Description
You have a grid of size n x 3 and you want to paint each cell of the grid with exactly one of the three colors: Red, Yellow, or Green while making sure that no two adjacent cells have the same color (i.e., no two cells that share vertical or horizontal sides have the same color).↳
Given n the number of rows of the grid, return the number of ways you can paint this grid. As the answer may grow large, the answer must be computed modulo 109 + 7.↳
Example 1:
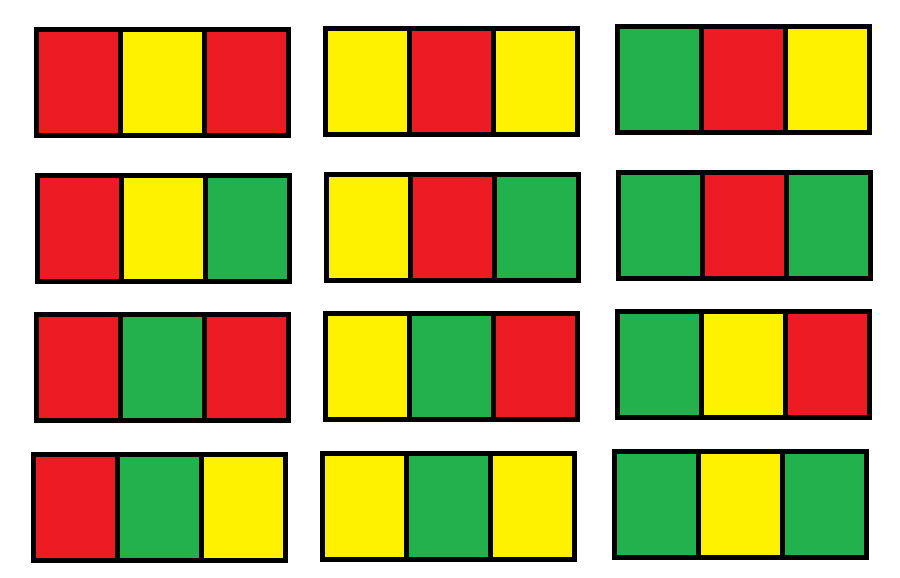
Input: n = 1 Output: 12 Explanation: There are 12 possible way to paint the grid as shown.
Example 2:
Input: n = 5000 Output: 30228214
Constraints:
n == grid.length1 <= n <= 5000
Code
DP = DFS + memoization
Time Complexity: , Space Complexity:
以 row 為單位去做 DFS,而非一個一個格子做。
class Solution {
int dp[5001][4][4][4] = {};
public:
int numOfWays(int n) {
return dfs(n, 0, 0, 0);
}
int dfs(int i, int a0, int b0, int c0) {
if(i == 0) return 1;
if(dp[i][a0][b0][c0] != 0) return dp[i][a0][b0][c0];
int ans = 0;
vector<int> colors = {1, 2, 3};
for(int a: colors) {
if(a == a0) continue;
for(int b: colors) {
if(b == b0 || b == a) continue;
for(int c: colors) {
if(c == c0 || c == b) continue;
ans += dfs(i - 1, a, b, c);
ans %= 1000000007;
}
}
}
return dp[i][a0][b0][c0] = ans;
}
};DP with constant space
Two pattern for each row, 121 and 123.
121, the first color same as the third in a row.
123, one row has three different colors.
We consider the state of the first row,
pattern 121: 121, 131, 212, 232, 313, 323.
pattern 123: 123, 132, 213, 231, 312, 321.
So we initialize a121 = 6, a123 = 6.
We consider the next possible for each pattern:
Patter 121 can be followed by: 212, 213, 232, 312, 313
Patter 123 can be followed by: 212, 231, 312, 232
121 => three 121, two 123
123 => two 121, two 123
So we can write this dynamic programming transform equation:
b121 = a121 * 3 + a123 * 2
b123 = a121 * 2 + a123 * 2
We calculate the result iteratively
and finally return the sum of both pattern a121 + a123
Time Complexity: , Space Complexity:
class Solution {
public:
int numOfWays(int n) {
long a121 = 6, a123 = 6, b121, b123, mod = 1e9 + 7;
for (int i = 1; i < n; ++i) {
b121 = a121 * 3 + a123 * 2;
b123 = a121 * 2 + a123 * 2;
a121 = b121 % mod;
a123 = b123 % mod;
}
return (a121 + a123) % mod;
}
};