Longest Increasing Path in a Matrix

Description

Given an m x n integers matrix, return the length of the longest increasing path in matrix.

From each cell, you can either move in four directions: left, right, up, or down. You may not move diagonally or move outside the boundary (i.e., wrap-around is not allowed).

Example 1:

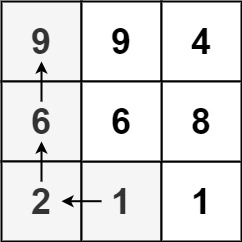
Input: matrix = [[9,9,4],[6,6,8],[2,1,1]] Output: 4 Explanation: The longest increasing path is [1, 2, 6, 9].

Example 2:

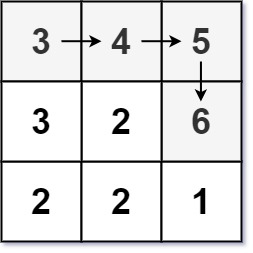
Input: matrix = [[3,4,5],[3,2,6],[2,2,1]] Output: 4 Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.

Example 3:

Input: matrix = 1 Output: 1

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= 231 - 1

Code

Topological Sort in a DAG

Time Complexity: $O(m+n)$, Space Complexity: $O(m+n)$

We regard

• a cell in the matrix as a node,
• a directed edge from node x to node y if x and y are adjacent and x’s value < y’s value

Then a graph is formed.

No cycles can exist in the graph, i.e. a DAG is formed.

The problem becomes to get the longest path in the DAG.

Topological sort can iterate the vertices of a DAG in the linear ordering.

Using Kahn’s algorithm(BFS) to implement topological sort while counting the levels can give us the longest chain of nodes in the DAG.

DFS with memo

Time Complexity: $O(m+n)$, Space Complexity: $O(m+n)$

class Solution {
    vector<vector<int>> dp;
    int res = 0;
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        int n = matrix.size();
        int m = matrix[0].size();
        dp.resize(n);
        for(int i = 0; i < n; i++) {
            dp[i].resize(m);
        }
 
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < m; j++) {
                dp[i][j] = -1;
            }
        }
 
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < m; j++) {
                res = max(res, dfs(matrix, i, j));
            }
        }
        
        return res;
    }
 
    int dfs(vector<vector<int>>& matrix, int i, int j) {
        int n = matrix.size();
        int m = matrix[0].size();
        if(dp[i][j] != -1) return dp[i][j];
 
        vector<vector<int>> dir = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};
        int temp = 0;
        for(int k = 0; k < 4; k++) {
            int x = i + dir[k][0];
            int y = j + dir[k][1];
            if(x < 0 || x >= n || y < 0 || y >= m) continue;
            if(matrix[i][j] >= matrix[x][y]) continue;
            temp = max(temp, dfs(matrix, x, y));
        }
        dp[i][j] = 1 + temp;
        return 1 + temp;
 
 
    }
};

Source

• Longest Increasing Path in a Matrix - LeetCode