Out of Boundary Paths

Description

There is an m x n grid with a ball. The ball is initially at the position [startRow, startColumn]. You are allowed to move the ball to one of the four adjacent cells in the grid (possibly out of the grid crossing the grid boundary). You can apply at most maxMove moves to the ball.

Given the five integers m, n, maxMove, startRow, startColumn, return the number of paths to move the ball out of the grid boundary. Since the answer can be very large, return it modulo 109 + 7.

Example 1:

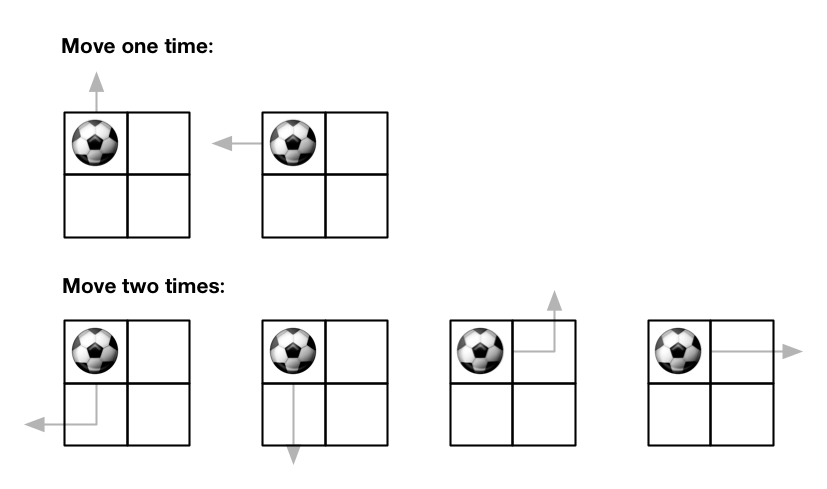
Input: m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0 Output: 6

Example 2:

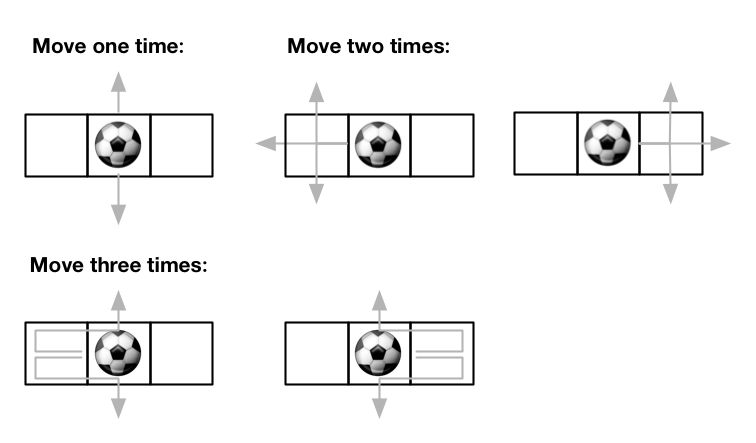
Input: m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1 Output: 12

Constraints:

• 1 <= m, n <= 50
• 0 <= maxMove <= 50
• 0 <= startRow < m
• 0 <= startColumn < n

Code

Top Down DP with memoization

Time Complexity: $O(mnM)$, Space Complexity: $O(mnM)$

不用擔心會不會走重複的路，因為這本來就是題目所允許的，一顆球可以左右滾動，最後在步數的限制之內 go out of bounds。

class Solution {
    int _n;
    int _m;
    int _maxMove;
    int dp[51][51][51];
 
public:
    int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
        _n = n;
        _m = m;
        _maxMove = maxMove;
        memset(dp, -1, sizeof(dp));
        return dfs(startRow, startColumn, 0);
    }
 
    int dfs(int i, int j, int move) {
        if((i >= _m) || (i < 0) || (j >= _n) || (j < 0)) {
            return 1;
        }
 
        if(dp[i][j][move] != -1) return dp[i][j][move];
 
        long long res = 0;
        if(move + 1 <= _maxMove) {
            res += (dfs(i + 1, j, move + 1) % 1000000007);
            res += (dfs(i - 1, j, move + 1) % 1000000007);
            res += (dfs(i, j + 1, move + 1) % 1000000007);
            res += (dfs(i, j - 1, move + 1) % 1000000007);
        }
        
        return dp[i][j][move] = (res % 1000000007);
    }
};

Source

• Out of Boundary Paths - LeetCode