Height of Binary Tree After Subtree Removal Queries

Description

You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.

You have to perform m independent queries on the tree where in the ith query you do the following:

• Remove the subtree rooted at the node with the value queries[i] from the tree. It is guaranteed that queries[i] will not be equal to the value of the root.

Return an array answer of size m where answer[i] is the height of the tree after performing the ith query.

Note:

• The queries are independent, so the tree returns to its initial state after each query.
• The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.

Example 1:

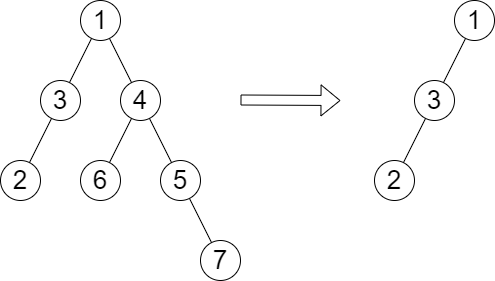
Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4] Output: [2] Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4. The height of the tree is 2 (The path 1 → 3 → 2).

Example 2:

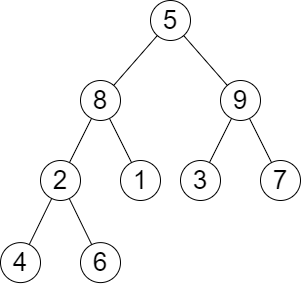
Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8] Output: [3,2,3,2] Explanation: We have the following queries:

• Removing the subtree rooted at node with value 3. The height of the tree becomes 3 (The path 5 → 8 → 2 → 4).
• Removing the subtree rooted at node with value 2. The height of the tree becomes 2 (The path 5 → 8 → 1).
• Removing the subtree rooted at node with value 4. The height of the tree becomes 3 (The path 5 → 8 → 2 → 6).
• Removing the subtree rooted at node with value 8. The height of the tree becomes 2 (The path 5 → 9 → 3).

Constraints:

• The number of nodes in the tree is n.
• 2 <= n <= 105
• 1 <= Node.val <= n
• All the values in the tree are unique.
• m == queries.length
• 1 <= m <= min(n, 104)
• 1 <= queries[i] <= n
• queries[i] != root.val

Code

Thinking Process:

1. 每一次 query，暴力解都是重新從 root traverse 一次，就可得到答案
2. 是否可以 pre compute？可以，height 和 depth 都可以，兩者合起來就是答案
3. 面對一個 query ，誰會是 candidate node？就是該 node 的 cousins(所有同 depth 的 node)
4. 是否還有 optimize 的空間？有，我們只會需要至多一個該 node 的替代人選

TLE 版本（how to optimize ? 我們只會需要至多一個該 node 的替代人選）

Time Complexity: $O(N)$, Space Complexity: $O(N)$

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int, vector<int>> cousins;
    unordered_map<int, int> depth;
    unordered_map<int, int> height;
    vector<int> treeQueries(TreeNode* root, vector<int>& queries) {
        int _ = dfs(root, 0); // build depth and height;
        // build cousins
        for(auto [node, d]: depth) {
            cousins[d].push_back(node);
        }
 
        vector<int> res;
        for(auto & q: queries) {
            int curr_depth = depth[q];
            int curr_h = curr_depth - 1;
            for(auto & c: cousins[curr_depth]) {
                if (c == q) {
                    continue;
                }
                curr_h = max(curr_h, depth[c] + height[c] - 1);
            }
            res.push_back(curr_h);
        }
        return res;
    }
    
    int dfs(TreeNode* root, int level) {
        if(!root) {
            return 0;
        }
        depth[root->val] = level;
        auto l = dfs(root->left, level + 1);
        auto r = dfs(root->right, level + 1);
        return height[root->val] = max(l, r) + 1;
    }
};

Optimal Solution

差別只在於原本的 unordered_map<int, vector<int>> cousins; 裝的是一個 node 對應的所有 cousin 的 node index，現在， unordered_map<int, vector<pair<int, int>>> cousins; 裝的是一個 node 對應的所有 cousin 的 height 和 node index ，且必須保持 height 是 sorted，size 不超過 2。

	/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int, vector<pair<int, int>>> cousins;
    unordered_map<int, int> depth;
    unordered_map<int, int> height;
    vector<int> treeQueries(TreeNode* root, vector<int>& queries) {
        int _ = dfs(root, 0); // build depth and height;
        // build cousins
        for(auto [node, d]: depth) {
            cousins[d].push_back({height[node], node});
            sort(begin(cousins[d]), end(cousins[d]), greater<pair<int, int>>());
            if(cousins[d].size() > 2) {
                cousins[d].pop_back();
            }
        }
 
        vector<int> res;
        for(auto & q: queries) {
            int curr_depth = depth[q];
            int curr_h = curr_depth - 1;
            for(auto & [h, c]: cousins[curr_depth]) {
                if (c == q) {
                    continue;
                }
                curr_h = max(curr_h, depth[c] + h - 1);
            }
            res.push_back(curr_h);
        }
        return res;
    }
 
    int dfs(TreeNode* root, int level) {
        if(!root) {
            return 0;
        }
        depth[root->val] = level;
        auto l = dfs(root->left, level + 1);
        auto r = dfs(root->right, level + 1);
        return height[root->val] = max(l, r) + 1;
    }
};

Source

• Height of Binary Tree After Subtree Removal Queries - LeetCode