Jimmy Lin's Blog

Search

SearchSearch

Frog Jump II

Jul 16, 2023, 4 min read

Description

You are given a 0-indexed integer array stones sorted in strictly increasing order representing the positions of stones in a river.

A frog, initially on the first stone, wants to travel to the last stone and then return to the first stone. However, it can jump to any stone at most once.

The length of a jump is the absolute difference between the position of the stone the frog is currently on and the position of the stone to which the frog jumps.

  • More formally, if the frog is at stones[i] and is jumping to stones[j], the length of the jump is |stones[i] - stones[j]|.

The cost of a path is the maximum length of a jump among all jumps in the path.

Return the minimum cost of a path for the frog.

Example 1:

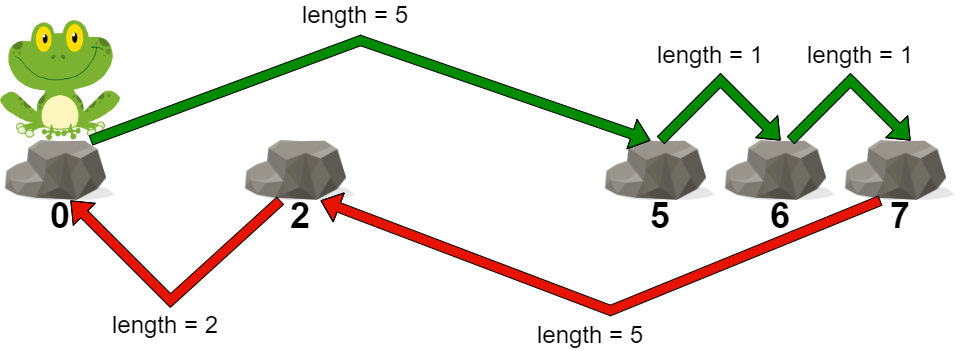
Input: stones = [0,2,5,6,7] Output: 5 Explanation: The above figure represents one of the optimal paths the frog can take. The cost of this path is 5, which is the maximum length of a jump. Since it is not possible to achieve a cost of less than 5, we return it.

Example 2:

Input: stones = [0,3,9] Output: 9 Explanation: The frog can jump directly to the last stone and come back to the first stone. In this case, the length of each jump will be 9. The cost for the path will be max(9, 9) = 9. It can be shown that this is the minimum achievable cost.

Constraints:

  • 2 <= stones.length <= 105
  • 0 <= stones[i] <= 109
  • stones[0] == 0
  • stones is sorted in a strictly increasing order.

Code

Time Complexity: , Space Complexity: 基本概念同：Binary Search 101。

由 camJump function 的 implementation 可看出進一步優化成 greedy 的方法。

在 canJump 當中，我們測試最大 jump 距離（threshold）是否可以讓青蛙來回跳完，而為了要讓青蛙在回程的路上是比較好跳回來的（距離較短），我們應該在去程的時候選擇距離較遠的下一 hop：

while(j + 1 < n && (stones[j + 1] - stones[i]) <= threshold) j++;

而這即是 Greedy 的 intuition，也就是說，應該要讓去程和回程的 jump 都剛好間隔為一：forward、backward、forward、backward、…，如此一來每個 jump 的距離才會被 minimized，若改成 forward、backward、backward、forward，則兩個 forward jump 之間的距離就會變大，path cost 就會變大。

因此，我們要找的就是 stones[i + 2] - stones[i] 的 max，即會是 min path cost。

class Solution {
public:
    int maxJump(vector<int>& stones) {
        int n = stones.size();
        int l = stones[1] - stones[0], r = stones.back() - stones[0];
        while(l < r) {
            int m = l + (r - l + 1) / 2;
            if(camJump(stones, m)) {
                r = m - 1;
            } else {
                l = m;
            }
        }
        return camJump(stones, r) ? r : r + 1;
    }
 
    bool camJump(vector<int> &stones, int threshold){
        int i = 0, n = stones.size();
        vector<bool> visited(n, false);
        while(i < n - 1) {
            int j = i;
            while(j + 1 < n && (stones[j + 1] - stones[i]) <= threshold) {
                j++;
            }
            if(j == i) return false;
            i = j;
            visited[i] = true;
        }
 
        vector<int> backward;
        for(int i = 0; i < n - 1; i++) {
            if(visited[i] == false)
                backward.push_back(i);
        }
        backward.push_back(n - 1);
 
        i = backward.size() - 1;
        while(i > 0) {
            int j = i;
            while(j > 0 && (stones[backward[i]] - stones[backward[j - 1]]) <= threshold) {
                j--;
            }
            if(j == i) return false;
            i = j;
        }
 
        return true;
    } 
 
    
};

注意 Binary Search 也可以寫成以下的形式：

while(l <= r) {
	int m = l + (r - l) / 2;
	if(camJump(stones, m)) {
		r = m - 1;
	} else {
		l = m + 1;
	}
}
return l;

Greedy

Time Complexity: , Space Complexity: 

class Solution {
public:
    int maxJump(vector<int>& stones) {
        int res = stones[1] - stones[0]; // edge case for only 2 elements
        for(int i = 0; i < stones.size() - 2; i++) {
            res = max(res, stones[i + 2] - stones[i]);
        }
        return res;
    }
};

Source

Graph View

Backlinks