Pizza With 3n Slices

Description

There is a pizza with 3n slices of varying size, you and your friends will take slices of pizza as follows:

• You will pick any pizza slice.
• Your friend Alice will pick the next slice in the anti-clockwise direction of your pick.
• Your friend Bob will pick the next slice in the clockwise direction of your pick.
• Repeat until there are no more slices of pizzas.

Given an integer array slices that represent the sizes of the pizza slices in a clockwise direction, return the maximum possible sum of slice sizes that you can pick.

Example 1:

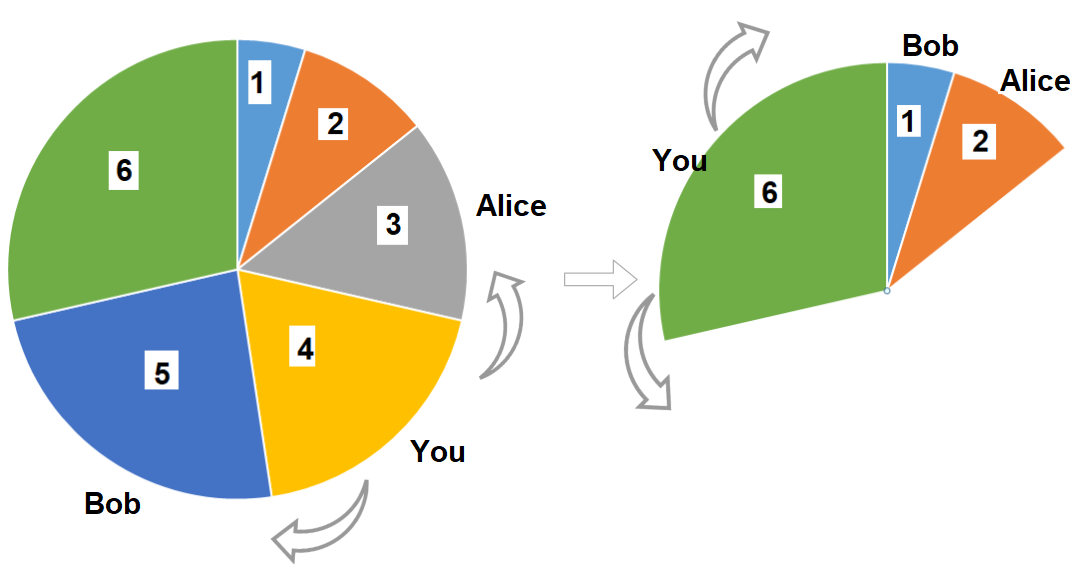
Input: slices = [1,2,3,4,5,6] Output: 10 Explanation: Pick pizza slice of size 4, Alice and Bob will pick slices with size 3 and 5 respectively. Then Pick slices with size 6, finally Alice and Bob will pick slice of size 2 and 1 respectively. Total = 4 + 6.

Example 2:

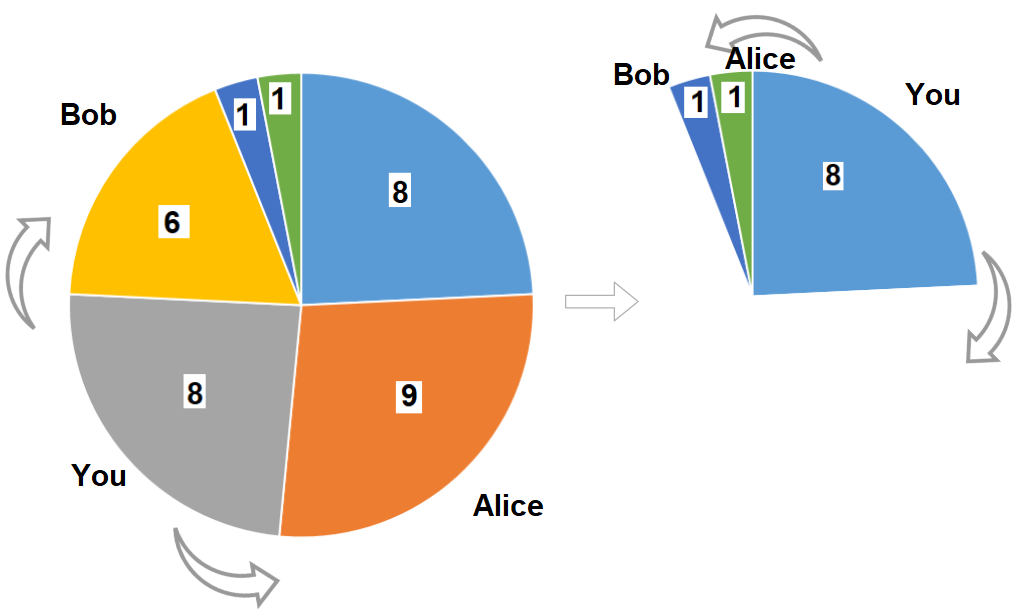
Input: slices = [8,9,8,6,1,1] Output: 16 Explanation: Pick pizza slice of size 8 in each turn. If you pick slice with size 9 your partners will pick slices of size 8.

Constraints:

• 3 * n == slices.length
• 1 <= slices.length <= 500
• 1 <= slices[i] <= 1000

Code

Brute Force - TLE

Time Complexity: $O(n!)$, Space Complexity: $O(n)$

class Solution {
    int res = INT_MIN;
public:
    int maxSizeSlices(vector<int>& slices) {
        unordered_set<int> used;
        solve(slices, 0, used);
        return res;
    }
 
    void solve(vector<int>& slices, int sum, unordered_set<int>& used) {
 
        if(used.size() == slices.size()) {
            res = max(res, sum);
            return;
        }
 
        for(int i = 0; i < slices.size(); i++) {
            if(!used.count(i)) {
                int alice = i;
                while(used.size() < slices.size()) {
                    alice = ((alice - 1) + slices.size()) % slices.size();
                    if(!used.count(alice)) break;
                }
 
                int bob = i;
                while(used.size() < slices.size()) {
                    bob = (bob + 1) % slices.size();
                    if(!used.count(bob)) break;
                }
                used.insert(i);
                used.insert(alice);
                used.insert(bob);
 
                solve(slices, sum + slices[i], used);
 
                used.erase(i);
                used.erase(alice);
                used.erase(bob);
            }
                
        }
    }
};

但是這個解法的 memoization 不知道該從何下手。

DP with memoization

Intuition：House Robber II。

Time Complexity: $O(n^2)$, Space Complexity: $O(n)$

class Solution {
    int memo[501][170];
 
public:
    int maxSizeSlices(vector<int>& slices) {
        int n = slices.size();
 
        // ignore the first one
        memset(memo, -1, sizeof(memo));
        int p1 = solve(1, n / 3, slices);
 
        // ignore the last one
        memset(memo, -1, sizeof(memo));
        slices[n-1] = 0;
        int p2 = solve(0, n / 3, slices);
 
        return max(p1, p2);
 
 
    }
 
    int solve(int i, int n, vector<int>& slices) {
 
        if(i >= slices.size() || n == 0) return 0;
        if(memo[i][n] != -1) return memo[i][n];
 
        return memo[i][n] = max(solve(i + 1, n, slices), slices[i] + solve(i + 2, n - 1, slices));
 
    }
};

Source

• Pizza With 3n Slices - LeetCode