K Closest Points to Origin

Description

Given an array of points where points[i] = [xi, yi] represents a point on the X-Y plane and an integer k, return the k closest points to the origin (0, 0).

The distance between two points on the X-Y plane is the Euclidean distance (i.e., √(x1 - x2)2 + (y1 - y2)2).

You may return the answer in any order. The answer is guaranteed to be unique (except for the order that it is in).

Example 1:

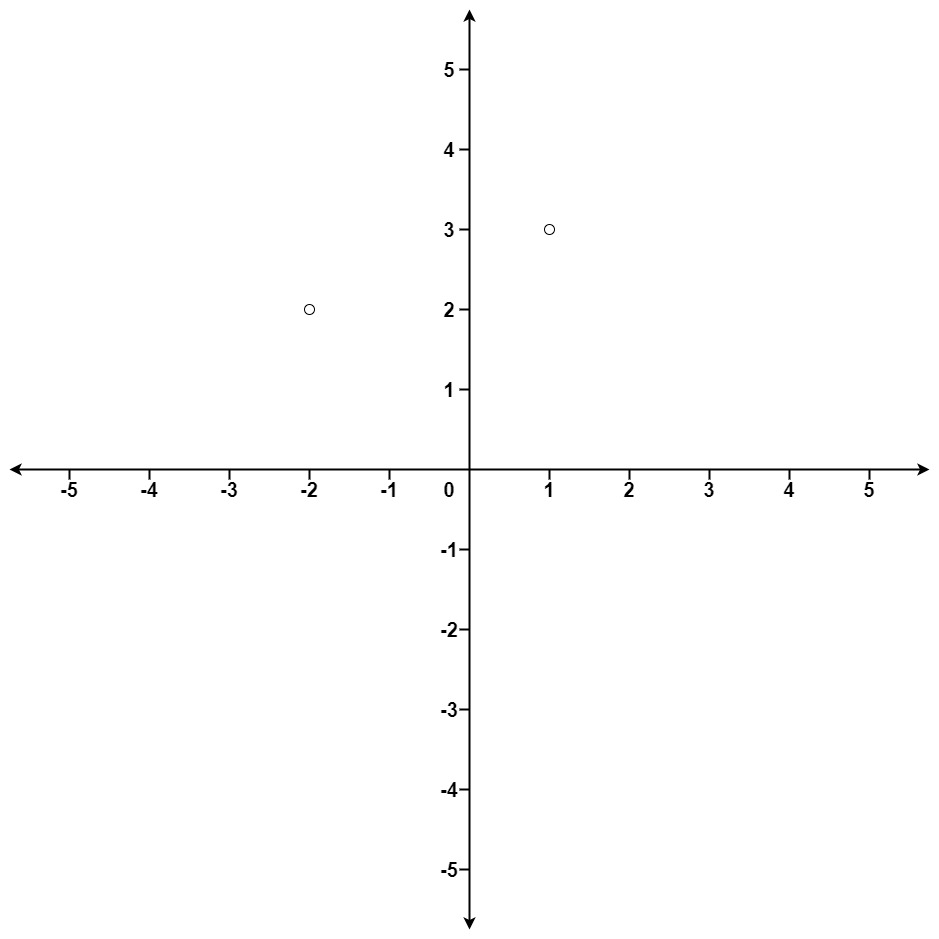
Input: points = [[1,3],[-2,2]], k = 1 Output: -2,2 Explanation: The distance between (1, 3) and the origin is sqrt(10). The distance between (-2, 2) and the origin is sqrt(8). Since sqrt(8) < sqrt(10), (-2, 2) is closer to the origin. We only want the closest k = 1 points from the origin, so the answer is just -2,2.

Example 2:

Input: points = [[3,3],[5,-1],[-2,4]], k = 2 Output: [[3,3],[-2,4]] Explanation: The answer [[-2,4],[3,3]] would also be accepted.

Constraints:

• 1 <= k <= points.length <= 104
• -104 < xi, yi < 104

Code

priority_queue & multiset 的不同在於，要 implement max heap 時的 operator 在 priority_queue 中是 < 但是在 multiset 中是 >。

priority_queue (Max Heap)

Time Complexity: $O(n\log k)$, Space Complexity: $O(k)$

注意 compare 的寫法：

參考：std::priority_queue

// Using a custom function object to compare elements.
    struct
    {
        bool operator() (const int l, const int r) const { return l > r; }
    } customLess;

class Solution {
public:
    vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
	    // max heap
        priority_queue<vector<int>, vector<vector<int>>, compare> pq;
        for(auto& point: points) {
            pq.push(point);
            if(pq.size() > k) pq.pop();
        }
        vector<vector<int>> answer;
        while(!pq.empty()) {
            answer.push_back(pq.top());
            pq.pop();
        }
        return answer;
    }
 
private:
    struct compare {
        bool operator()(vector<int>& p, vector<int>& q) {
        // max heap
            return p[0] * p[0] + p[1] * p[1] < q[0] * q[0] + q[1] * q[1];
        }
    };
 
};

multiset

Time Complexity: $O(n\log k)$, Space Complexity: $O(k)$

參考：std::multiset, std::copy_n, std::back_inserter

class Solution {
public:
    vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
        multiset<vector<int>, compare> mset;
        for(auto& point: points) {
            mset.insert(point);
            if (mset.size() > k) {
            // since ordering is from max to min
            // we pop the max
                mset.erase(mset.begin());
            }
        }
        vector<vector<int>> answer;
        copy_n(mset.begin(), k, back_inserter(answer));
        return answer;
    }
 
private:
    struct compare {
        bool operator()(const vector<int>& p, const vector<int>& q) const {
        // order from max to min
            return p[0] * p[0] + p[1] * p[1] > q[0] * q[0] + q[1] * q[1];
        }
    };
 
};

注意 partial_sort 和 nth_element 的 iterator 的 index 不一樣，在 nth_element 中是 points.begin() + k - 1 的原因是：

nth_element is a partial sorting algorithm that rearranges elements in [first, last) such that:

The element pointed at by nth is changed to whatever element would occur in that position if [first, last) were sorted.

partial_sort

Time Complexity: $O(n)$, Space Complexity: $O(n)$

• std::partial_sort

class Solution {
public:
    vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
        partial_sort(points.begin(), points.begin() + k, points.end(), [](vector<int>& p, vector<int>& q){return p[0] * p[0] + p[1] * p[1] < q[0] * q[0] + q[1] * q[1];});
        return vector<vector<int>>(points.begin(), points.begin() + k);
    }
};

nth_element

Time Complexity: $O(n)$, Space Complexity: $O(n)$

• std::nth_element

class Solution {
public:
    vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
        nth_element(points.begin(), points.begin() + k - 1, points.end(), [](vector<int>& p, vector<int>& q){return p[0] * p[0] + p[1] * p[1] < q[0] * q[0] + q[1] * q[1];});
        return vector<vector<int>>(points.begin(), points.begin() + k);
    }
};

Source

• K Closest Points to Origin - LeetCode