Jimmy Lin's Blog

Search

SearchSearch

Binary Search 101

Jul 01, 2023, 19 min read

中文翻譯（由 GPT-4 提供）

二分搜尋通常是一個易於在抽象層面解釋的主題，但是當涉及到寫無錯誤的實現時，卻相當困難。

一些最常見的問題包括：

  1. 無窮迴圈
  2. 無法決定在哪裡收縮範圍
  3. 應該使用低端還是高端索引
  4. 何時退出迴圈
  5. …

在本文中，我將分享我的見解，關於如何用一點點的模式寫出無錯誤的二分搜尋。

如果你對二分搜尋已經熟悉，只想看模式，你可以直接跳到部分：模式。

什麼是二分搜尋？

通常，要在一組中找到目標，比如一組數字的陣列，最糟糕的情況是我們需要逐一檢查每個元素（O(n)）。然而，當這些元素已排序，我們可以利用這個額外的資訊將搜尋時間降低到 O(log n)，也就是說，如果我們有100個元素，最壞的情況下需要進行10次搜尋。這是一個巨大的性能提升。

下面的 Gif 展示了二分搜尋的威力。

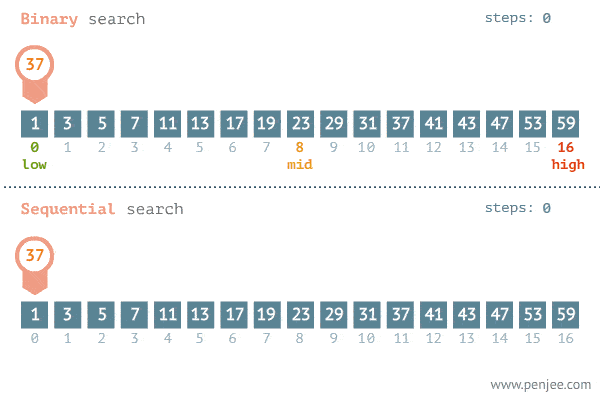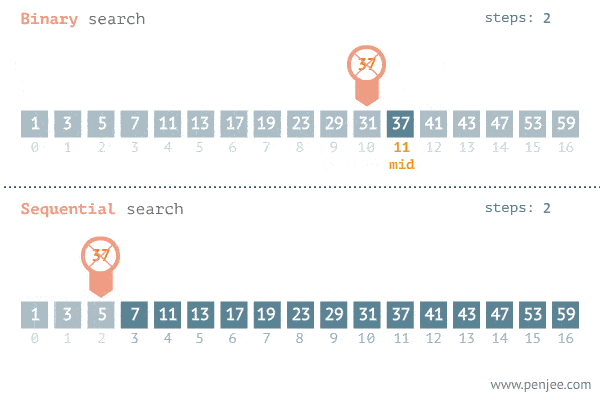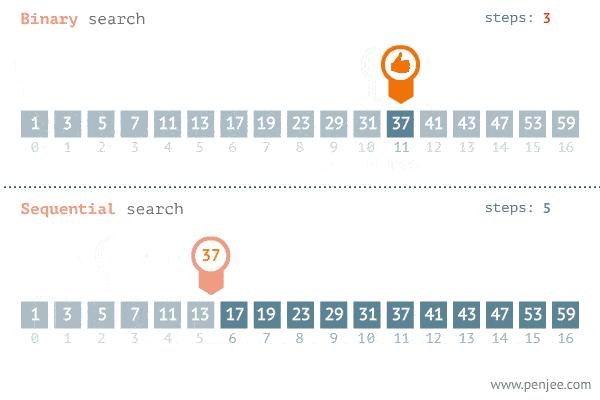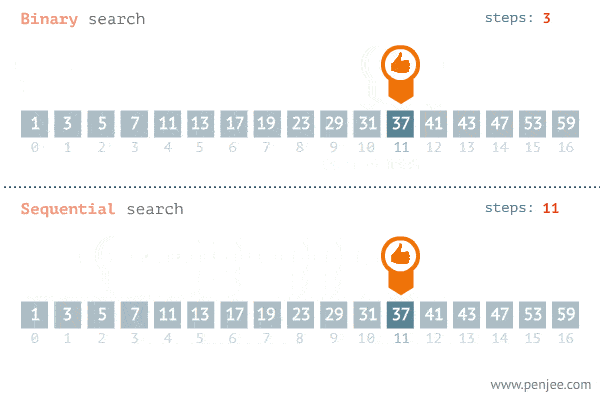
https://assets.leetcode.com/static_assets/posts/1EYkSkQaoduFBhpCVx7nyEA.gif

這種巨大的性能提升的原因是因為在每一次搜尋迭代中，我們能將將要查看的元素減半。查看的元素越少 = 搜尋時間越快。這全部源於一個簡單的事實，即在排序的列表中，n 的右邊的所有元素都會大於或等於它，反之亦然。

在我們看二分搜尋的抽象概念之前，先讓我們看看代碼：

var search = function(nums, target) {
    let lo = 0, hi = nums.length-1;
    while (lo < hi) {
        let mid = lo + Math.floor((hi-lo+1)/2);
        if (target < nums[mid]) {
            hi = mid - 1
        } else {
            lo = mid; 
        }
    }
    return nums[lo]==target?lo:-1;
};

1. lo & hi
我們定義了兩個變數，我們叫他們 lo 和 hi 。他們會存儲陣列索引，並像一個邊界那樣工作，這樣我們只會看邊界內的元素。
通常，我們希望將邊界初始化為整個陣列。

let lo = 0, hi = nums.length-1;

2. mid
mid 變數表示在邊界內的中間元素。它將我們的邊界分為兩部分。記住我說過二分搜尋的工作原理是不斷將元素切半，mid 元素就像一個交通警察，它指示我們要將邊界切割到哪一邊。

注意當一個陣列有偶數個元素時，你可以選擇使用左邊的 mid（較低的 mid）或者右邊的 mid（較高的 mid）

let mid = lo + Math.floor((hi - lo) / 2); // left/lower mid
 
let mid = lo + Math.floor((hi - lo + 1) / 2); // right/upper mid

3. 將目標與 mid 進行比較
通過將我們的目標與 mid 進行比較，我們可以確定目標屬於邊界的哪一邊。例如，如果我們的目標大於 mid，這意味著它必須存在於 mid 的右邊。在這種情況下，我們甚至沒有理由記錄它左邊的所有數字。這就是二分搜尋的基本機制 - 不斷縮小邊界。

if (target < nums[mid]) {
	hi = mid - 1
} else {
	lo = mid; 
}

4. 保持迴圈運行
最後，我們使用一個 while 迴圈來保持搜尋的進行：

當 lo == hi 時，while 迴圈才會退出，這意味著只剩下一個元素。如果我們的實現都是正確的，那麼這個唯一的元素應該就是我們的答案（假設目標在陣列中）。

模式

二分搜尋看起來可能是一個很簡單的概念，但是當你仔細看代碼時，我們正在做一些重要的決定，這些決定可以完全改變我們的代碼的行為。
這些決定包括：

  1. 我應該使用左邊還是右邊的 mid？
  2. 我應該使用 < 或 <=， > 或 >=？
  3. 我應該縮小多少邊界？是 mid 還是 mid - 1，或者甚至是 mid + 1？
  4. …

而只要搞砸了這些決定中的一個，無論是因為你完全不理解它，還是因為錯誤，都會讓你的代碼崩潰。
為瞭解決這些決策問題，我使用以下的一套規則來始終讓我遠離麻煩，最重要的是，它使我的代碼在所有的邊緣情況下更加一致和可預測。

1. lo 和 hi 的選擇，也就是邊界
通常，我們將初始邊界設定為陣列中的元素數量

let lo = 0, hi = nums.length;

但這並不總是如此。
我們需要記住：邊界是我們將從中進行搜尋的元素的範圍。
初始邊界應該包括所有元素，也就是說所有可能的答案應該都被包括在內。二分搜尋可以應用於非陣列問題，例如數學問題，這個聲明依然有效。

例如，在 LeetCode 35 中，該問題要我們找到一個索引來插入到陣列中。
我們可能會在陣列的最後一個元素之後插入，因此完整的邊界範圍變為

let mid = Math.floor((lo + hi) / 2) // 最差，非常容易溢位
 
let mid = lo + Math.floor((hi - lo) / 2) // 好很多，但仍然可能
 
let mid = (lo + hi) >>> 1 // 最好，但難以理解

2. 計算 mid
當數字極大時，計算 mid 可能會導致溢位。我將從最差到最好演示幾種計算 mid 的方法。

let mid = lo + Math.floor((hi - lo) / 2) // left/lower mid
 
let mid = lo + Math.floor((hi - lo + 1) / 2) // right/upper mid

當我們處理偶數元素時，選擇左邊的 mid 或右邊的 mid 是我們的選擇，我將在後面的章節中解釋，一個錯誤的選擇會導致無窮迴圈。

if (target < nums[mid]) {
	hi = mid - 1
} else {
	lo = mid; 
}

3. 我們如何縮小邊界
我總是嘗試盡可能保持簡單的邏輯，也就是一對 if...else。但是我們在這裡使用的是什麼邏輯呢？我的經驗法則是總是使用一種可以排除 mid 的邏輯。
看一個例子：

if (target > nums[mid]) {
	lo = mid + 1; // mid 被排除
} else {
	hi = mid; // mid 被包括
}

在這裡，如果目標小於 mid，那麼 mid 絕不可能是我們的答案，我們可以很自信地使用 hi = mid - 1 排除它。否則，mid 仍然有可能是目標，因此我們將它包括在邊界 lo = mid 中。
另一方面，我們可以將邏輯重寫為：

if (target > nums[mid]) {
	lo = mid + 1; // mid 被排除
} else {
	hi = mid; // mid 被包括
}

4. while 迴圈
為了保持邏輯簡單，我總是使用

while(lo < hi) { ... }

為什麼？因為這樣，迴圈退出的唯一條件就是 lo == hi。我知道他們將指向同一個元素，而且我知道那個元素總是存在的。

5. 避免無窮迴圈
記得我說過，選擇左邊或右邊的 mid 的壞選擇會導致無窮迴圈嗎？讓我們解決這個問題。
範例：

let mid = lo + ((hi - lo) / 2); // Bad! 我們應該使用 right/upper mid!
 
if (target < nums[mid]) {
	hi = mid - 1
} else {
	lo = mid; 
}

現在，想像一下在邊界中只剩下兩個元素的情況。如果邏輯落入 else 語句，由於我們使用的是左邊/較低的 mid，它根本就沒有做任何事情。它只是不斷地將自己縮小到自己，程序卡住了。
我們必須記住，mid 的選擇和我們的縮小邏輯必須協同工作，每次至少排除一個元素。

let mid = lo + ((hi - lo + 1) / 2); // Bad! 我們應該使用 left/lower mid!
 
if (target > nums[mid]) {
	lo = mid + 1; // mid 被排除
} else {
	hi = mid; // mid 被包括
}

所以當你的二分搜尋卡住時，想想只剩下兩個元素的情況。邊界縮小得正確嗎？

總結

我對二分搜尋的經驗法則：

  1. 初始化 lo 和 hi 時，包括所有可能的答案
  2. 不要讓 mid 的計算溢位
  3. 使用可以排除 mid 的邏輯來縮小邊界
  4. 透過選擇正確的 mid 和縮小邏輯來避免無窮迴圈
  5. 總是考慮只剩下兩個元素的情況

由於這個問題相對簡單，所以實現可能相當直接，你可能會想，我為什麼需要這麼多規則。然而，二分搜尋的問題可以變得更複雜，沒有一致的規則，就很難寫出可預測的代碼。最後，我會說，每個人都有他們自己的二分搜尋風格，找到適合你的風格！

英文原版

Binary search is often a topic that’s easy to be explained on the abstract level, but when it comes to writing bug free implementations, it’s rather difficult.

Some of the most common problems include:

  1. Infinity loop
  2. Can’t decide where to shrink
  3. Do I use lo or hi
  4. When to exit the loop
  5. …

In this article, I will be sharing my insights on how to write bug free binary search with just a little pattern.

If you are familiar with binary search and just want to see the pattern, you can go directly to the part: The Pattern.

Normally, to find the target in a group, such as an array of numbers, the worst case scenario is we need to go through every single element (O(n)). However, when these elements are sorted, we are able to take the privilege of this extra information to bring down the search time to O(log n), that is if we have 100 elements, the worst case scenario would be 10 searches. That is a huge performance improvement.

The Gif below demonstrates the power of binary search.

https://assets.leetcode.com/static_assets/posts/1EYkSkQaoduFBhpCVx7nyEA.gif

The reason behind this huge performance increase is because for each search iterations, we are able to cut the elements we will be looking at in half. Fewer elements to look at = faster search time. And this all comes from the simple fact that in a sorted list, everything to the right of n will be greater or equal to it, and vice versa.

Before we look at the abstract ideas of binary search, let’s see the code first:

var search = function(nums, target) {
    let lo = 0, hi = nums.length-1;
    while (lo < hi) {
        let mid = lo + Math.floor((hi-lo+1)/2);
        if (target < nums[mid]) {
            hi = mid - 1
        } else {
            lo = mid; 
        }
    }
    return nums[lo]==target?lo:-1;
};

The fundamental idea

1. lo & hi
We define two variables, let’s call them lo and hi . They will store array indexes and they work like a boundary such that we will only be looking at elements inside the boundary.
Normally, we would want initialize the boundary to be the entire array.

let lo = 0, hi = nums.length-1;

2. mid
The mid variable indicates the middle element within the boundary. It separates our boundary into 2 parts. Remember how I said binary search works by keep cutting the elements in half, the mid element works like a traffic police, it indicates us which side do we want to cut our boundary to.

Note when an array has even number of elements, it’s your decision to use either the left mid (lower mid) or the right mid (upper mid)

let mid = lo + Math.floor((hi - lo) / 2); // left/lower mid
 
let mid = lo + Math.floor((hi - lo + 1) / 2); // right/upper mid

3. Comparing the target to mid
By comparing our target to mid, we can identify which side of the boundary does the target belong. For example, If our target is greater than mid, this means it must exist in the right of mid . In this case, there is no reason to even keep a record of all the numbers to its left. And this is the fundamental mechanics of binary search - keep shrinking the boundary.

if (target < nums[mid]) {
	hi = mid - 1
} else {
	lo = mid; 
}

4. Keep the loop going
Lastly, we use a while loop to keep the search going:

The while loop only exits when lo == hi, which means there’s only one element left. And if we implemented everything correctly, that only element should be our answer(assume if the target is in the array).

The pattern

It may seem like binary search is such a simple idea, but when you look closely in the code, we are making some serious decisions that can completely change the behavior of our code.
These decisions include:

  1. Do I use left or right mid?
  2. Do I use < or <= , > or >=?
  3. How much do I shrink the boundary? is it mid or mid - 1 or even mid + 1 ?
  4. …

And just by messing up one of these decisions, either because you don’t understand it completely or by mistake, it’s going to break your code.
To solve these decision problems, I use the following set of rules to always keep me away from trouble, most importantly, it makes my code more consistent and predictable in all edge cases.

1. Choice of lo and hi, aka the boundary
Normally, we set the initial boundary to the number of elements in the array

let lo = 0, hi = nums.length - 1;

But this is not always the case.
We need to remember: the boundary is the range of elements we will be searching from.
The initial boundary should include ALL the elements, meaning all the possible answers should be included. Binary search can be applied to none array problems, such as Math, and this statement is still valid.

For example, In LeetCode 35, the question asks us to find an index to insert into the array.
It is possible that we insert after the last element of the array, thus the complete range of boundary becomes

let lo = 0, hi = nums.length;

2. Calculate mid
Calculating mid can result in overflow when the numbers are extremely big. I ll demonstrate a few ways of calculating mid from the worst to the best.

let mid = Math.floor((lo + hi) / 2) // worst, very easy to overflow
 
let mid = lo + Math.floor((hi - lo) / 2) // much better, but still possible
 
let mid = (lo + hi) >>> 1 // the best, but hard to understand

When we are dealing with even elements, it is our choice to pick the left mid or the right mid , and as I ll be explaining in a later section, a bad choice will lead to an infinity loop.

let mid = lo + Math.floor((hi - lo) / 2) // left/lower mid
 
let mid = lo + Math.floor((hi - lo + 1) / 2) // right/upper mid

3. How do we shrink boundary
I always try to keep the logic as simple as possible, that is a single pair of if...else. But what kind of logic are we using here? My rule of thumb is always use a logic that you can exclude mid.
Let’s see an example:

if (target < nums[mid]) {
	hi = mid - 1
} else {
	lo = mid; 
}

Here, if the target is less than mid, there’s no way mid will be our answer, and we can exclude it very confidently using hi = mid - 1. Otherwise, mid still has the potential to be the target, thus we include it in the boundary lo = mid.
On the other hand, we can rewrite the logic as:

if (target > nums[mid]) {
	lo = mid + 1; // mid is excluded
} else {
	hi = mid; // mid is included
}

4. while loop
To keep the logic simple, I always use

while(lo < hi) { ... }

Why? Because this way, the only condition the loop exits is lo == hi. I know they will be pointing to the same element, and I know that element always exists.

5. Avoid infinity loop
Remember I said a bad choice of left or right mid will lead to an infinity loop? Let’s tackle this down.
Example:

let mid = lo + ((hi - lo) / 2); // Bad! We should use right/upper mid!
 
if (target < nums[mid]) {
	hi = mid - 1
} else {
	lo = mid; 
}

Now, imagine when there are only 2 elements left in the boundary. If the logic fell into the else statement, since we are using the left/lower mid, it’s simply not doing anything. It just keeps shrinking itself to itself, and the program got stuck.
We have to keep in mind that, the choice of mid and our shrinking logic has to work together in a way that every time, at least 1 element is excluded.

let mid = lo + ((hi - lo + 1) / 2); // Bad! We should use left/lower mid!
 
if (target > nums[mid]) {
	lo = mid + 1; // mid is excluded
} else {
	hi = mid; // mid is included
}

So when your binary search is stuck, think of the situation when there are only 2 elements left. Did the boundary shrink correctly?

TD;DR

My rule of thumb when it comes to binary search:

  1. Include ALL possible answers when initialize lo & hi
  2. Don’t overflow the mid calculation
  3. Shrink boundary using a logic that will exclude mid
  4. Avoid infinity loop by picking the correct mid and shrinking logic
  5. Always think of the case when there are 2 elements left

Because this problem is a failrly easy, the implementions may be pretty straight forward and you may wonder why do I need so many rules. However, binary search problems can get much much more complex, and without consistent rules, it’s very hard to write predictable code. In the end, I would say everybody has their own style of binary serach, find the style that works for you!

Reference

Graph View

Backlinks