Number of Submatrices That Sum to Target

Description

Given a matrix and a target, return the number of non-empty submatrices that sum to target.

A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.

Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.

Example 1:

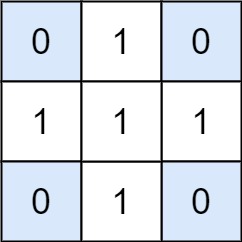
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0 Output: 4 Explanation: The four 1x1 submatrices that only contain 0.

Example 2:

Input: matrix = [[1,-1],[-1,1]], target = 0 Output: 5 Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.

Example 3:

Input: matrix = 904, target = 0 Output: 0

Constraints:

• 1 <= matrix.length <= 100
• 1 <= matrix[0].length <= 100
• -1000 <= matrix[i] <= 1000
• -10^8 <= target <= 10^8

Code

Subarray Sum Equals K 的 2D 版本。

和 Subarray Sum Equals K 中的概念相同，只要目前為止的 prefixSum 減去 k 之後的值是有出現過的，代表從目前這個位置，到之前有出現過的位置（可能有多個），中間的 subarray 其 sum 都等於 k。

res += mp[prefixSum[i] - k];

因此在這題中，我們有以下的程式碼：

res += counter.find(cur - target) != counter.end() ? counter[cur - target] : 0;

Time Complexity: $O(n^2)$, Space Complexity: $O(n^2)$

class Solution {
public:
    int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        for(int i = 0; i < m; i++)
            for(int j = 1; j < n; j++) 
                matrix[i][j] += matrix[i][j - 1];
        // i, j for col combinations
        // k for row index
        int res = 0;
        for(int i = 0; i < n; i++) {
            for(int j = i; j < n; j++) {
                unordered_map<int, int> count = {{0, 1}};
                int curSum = 0;
                for(int k = 0; k < m; k++) {
                    curSum += matrix[k][j] - (i > 0 ? matrix[k][i - 1] : 0);
                    if(count.find(curSum - target) != count.end()) {
                        res += count[curSum - target];
                    }
                    count[curSum]++;
                }
            }
        }
        return res;
    }
};

Source

• Number of Submatrices That Sum to Target - LeetCode