Range Sum Query - Mutable

Description

Given an integer array nums, handle multiple queries of the following types:

1. Update the value of an element in nums.
2. Calculate the sum of the elements of nums between indices left and right inclusive where left <= right.

Implement the NumArray class:

• NumArray(int[] nums) Initializes the object with the integer array nums.
• void update(int index, int val) Updates the value of nums[index] to be val.
• int sumRange(int left, int right) Returns the sum of the elements of nums between indices left and right inclusive (i.e. nums[left] + nums[left + 1] + ... + nums[right]).

Example 1:

<strong>Input</strong>
["NumArray", "sumRange", "update", "sumRange"]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
<strong>Output</strong>
[null, 9, null, 8]

<strong>Explanation</strong>
NumArray numArray = new NumArray([1, 3, 5]);
numArray.sumRange(0, 2); // return 1 + 3 + 5 = 9
numArray.update(1, 2);   // nums = [1, 2, 5]
numArray.sumRange(0, 2); // return 1 + 2 + 5 = 8

Constraints:

• 1 <= nums.length <= 3 * 10<sup>4</sup>
• -100 <= nums[i] <= 100
• 0 <= index < nums.length
• -100 <= val <= 100
• 0 <= left <= right < nums.length
• At most 3 * 10<sup>4</sup> calls will be made to update and sumRange.

Code

Time Complexity: $O(n)$, Space Complexity: $O(n)$

segment tree 背後的精神是 divide and conquer。

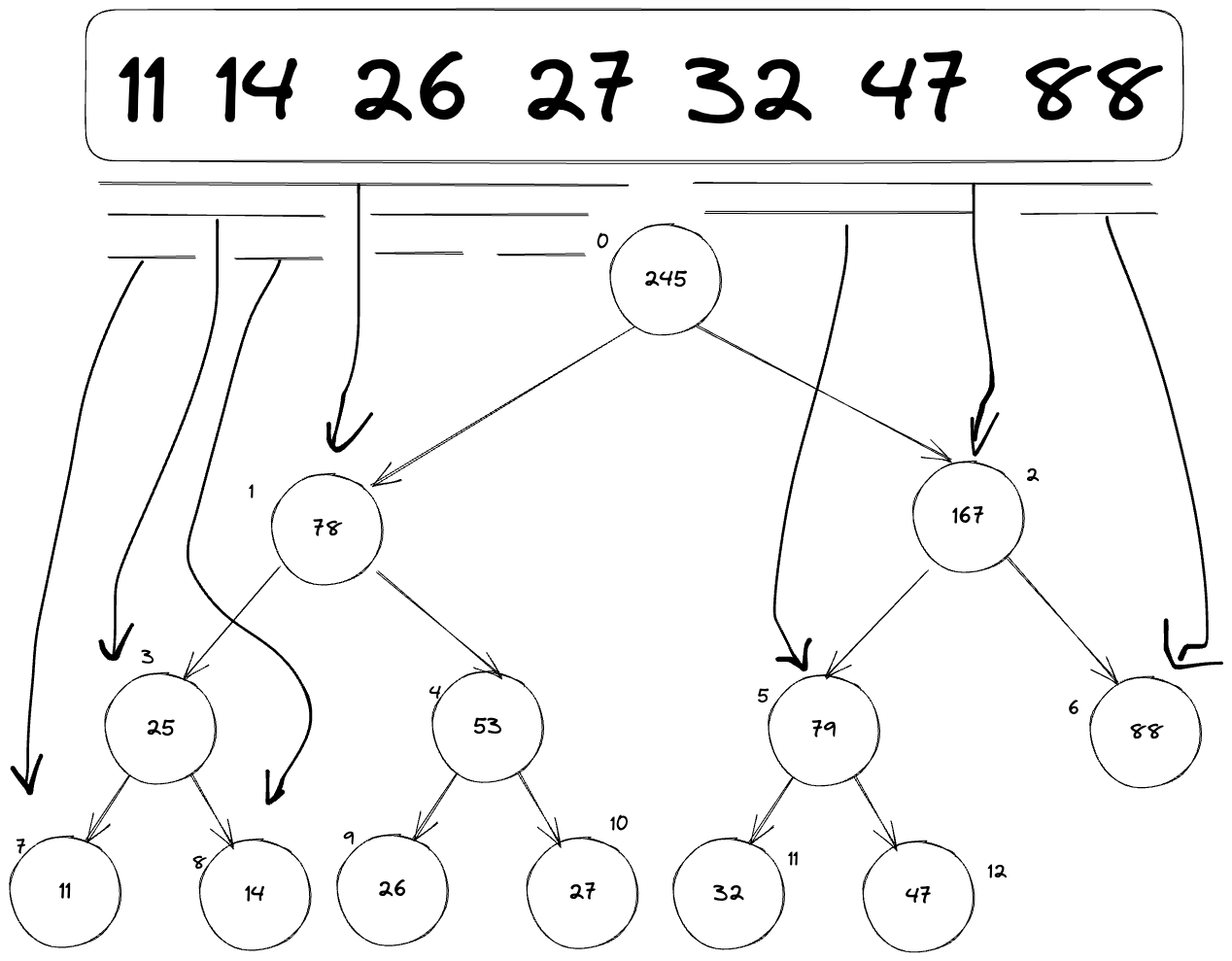
用原本的 array 的 left right mid 去做 divide and conquer，而 index parameter 是 for segment tree array 使用的，更新方式是 left child = 2 index + 1, right child = 2 index + 2(zero based)。

#define lc 2 * index + 1
#define rc 2 * index + 2
class NumArray {
    vector<int> A;
    vector<int> S;
public:
    int buildTree(int left, int right, int index) {
        if(left == right) 
            return S[index] = A[left];
        int mid = left + (right - left) / 2;
        return S[index] = buildTree(left, mid, lc) + buildTree(mid + 1, right, rc);
    }
 
    void updateTree(int t, int left, int right, int index, int data) {
        if(t < left || t > right) return;
        if(left == t && right == t) {
            S[index] = data;
            return;
        }
        int mid = left + (right - left) / 2;
        updateTree(t, left, mid, lc, data);
        updateTree(t, mid + 1, right, rc, data);
        S[index] = S[lc] + S[rc];
    }
 
    int query(int qleft, int qright, int left, int right, int index) {
        if(qleft > right || qright < left) return 0;
        else if(qleft <= left && right <= qright) return S[index];
        int mid = left + (right - left) / 2;
        return query(qleft, qright, left, mid, lc) + query(qleft, qright, mid + 1, right, rc);
    }
    
    NumArray(vector<int>& nums) {
        A = nums;
        int n = A.size();
        S.resize(4*n);
        buildTree(0, n - 1, 0);
    }
    
    void update(int index, int val) {
        updateTree(index, 0, A.size() - 1, 0, val);
    }
    
    int sumRange(int left, int right) {
        return query(left, right, 0, A.size() - 1, 0);
    }
};
 
/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * obj->update(index,val);
 * int param_2 = obj->sumRange(left,right);
 */

Source

• Range Sum Query - Mutable - LeetCode