Pseudo-Palindromic Paths in a Binary Tree

Description

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

Example 1:

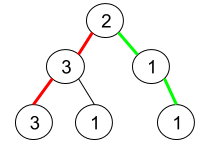
Input: root = [2,3,1,3,1,null,1] Output: 2 Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 2:

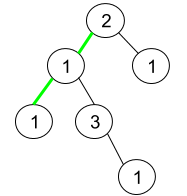
Input: root = [2,1,1,1,3,null,null,null,null,null,1] Output: 1 Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 3:

Input: root = [9] Output: 1

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 9

Code

重點都在於 if(oddCount <= 1) res++;，最多只能有一個偶數個的數字，要不然就排不成 Palindrome。剩下的只是該如何去紀錄有多少的數字是偶數個。

Use Array as Hashmap

Time Complexity: $O(N)$, Space Complexity: $O(N)$

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    int res = 0;
    vector<int> count;
public:
    int pseudoPalindromicPaths (TreeNode* root) {
        count.resize(10);
        check(root);
        return res;
    }
 
    void check(TreeNode* node) {
        count[node->val]++;
 
        if(!node->left && !node->right) {
            int oddCount = 0;
            for(auto c: count) {
                if(c % 2 == 1) oddCount++;
            }
            if(oddCount <= 1) res++;
        } else {
            if(node->left) check(node->left);
            if(node->right) check(node->right);
        }
        count[node->val]--;
    }
};

BitMask

At the leaf node,
check if the count has only one bit that is 1.

    int pseudoPalindromicPaths(TreeNode* root, int count = 0) {
        if (!root) return 0;
        count ^= 1 << (root->val - 1);
        int res = pseudoPalindromicPaths(root->left, count) + pseudoPalindromicPaths(root->right, count);
        if (root->left == root->right && (count & (count - 1)) == 0) res++;
        return res;
    }

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    int res = 0;
public:
    int pseudoPalindromicPaths (TreeNode* root) {
        if (!root) return 0;
        int count = 0;
        check(root, count);
        return res;
    }
 
    void check(TreeNode* node, int count) {
        count ^= 1 << (node->val - 1);
        if (!node->left && !node->right){
            if((count & (count - 1)) == 0) res++;
        } else {
            if(node->left) check(node->left, count);
            if(node->right) check(node->right, count);
        }
        count ^= 1 << (node->val - 1);
    }
};

Source

• Pseudo-Palindromic Paths in a Binary Tree - LeetCode