Get the Maximum Score

Description

You are given two sorted arrays of distinct integers nums1 and nums2.

A valid path is defined as follows:

• Choose array nums1 or nums2 to traverse (from index-0).
• Traverse the current array from left to right.
• If you are reading any value that is present in nums1 and nums2 you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).

The score is defined as the sum of uniques values in a valid path.

Return the maximum score you can obtain of all possible valid paths. Since the answer may be too large, return it modulo 109 + 7.

Example 1:

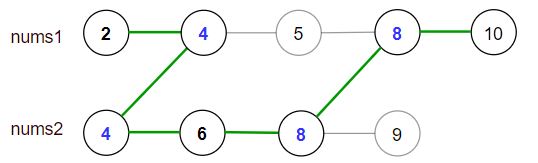
Input: nums1 = [2,4,5,8,10], nums2 = [4,6,8,9] Output: 30 Explanation: Valid paths: [2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10], (starting from nums1) [4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10] (starting from nums2) The maximum is obtained with the path in green [2,4,6,8,10].

Example 2:

Input: nums1 = [1,3,5,7,9], nums2 = [3,5,100] Output: 109 Explanation: Maximum sum is obtained with the path [1,3,5,100].

Example 3:

Input: nums1 = [1,2,3,4,5], nums2 = [6,7,8,9,10] Output: 40 Explanation: There are no common elements between nums1 and nums2. Maximum sum is obtained with the path [6,7,8,9,10].

Constraints:

• 1 <= nums1.length, nums2.length <= 105
• 1 <= nums1[i], nums2[i] <= 107
• nums1 and nums2 are strictly increasing.

Code

Time Complexity: $O(n)$, Space Complexity: $O(1)$

在傳送門之後上下兩線繼續前進累積值的 base 就是兩線累積至傳送門之前取 max。

class Solution {
public:
    int maxSum(vector<int>& nums1, vector<int>& nums2) {
        long m = nums1.size();
        long n = nums2.size();
        long i = 0, j = 0;
        long long x = 0, y = 0;
        long long M = 1e9 + 7;
 
        while(i < m || j < n) {
            if(i == m) {
                y += nums2[j];
                j++;
            } else if (j == n) {
                x += nums1[i];
                i++;
            } else if (nums1[i] < nums2[j]) {
                x += nums1[i];
                i++;
            } else if (nums1[i] > nums2[j]) {
                y += nums2[j];
                j++;
            } else if (nums1[i] == nums2[j]) {
                x = max(x, y) + nums1[i];
                y = x;
                i++;
                j++;
            }
        }
 
        return max(x, y) % M;
    }
};

Source

• Get the Maximum Score - LeetCode