Spiral Matrix III

Description

You start at the cell (rStart, cStart) of an rows x cols grid facing east. The northwest corner is at the first row and column in the grid, and the southeast corner is at the last row and column.

You will walk in a clockwise spiral shape to visit every position in this grid. Whenever you move outside the grid’s boundary, we continue our walk outside the grid (but may return to the grid boundary later.). Eventually, we reach all rows * cols spaces of the grid.

Return an array of coordinates representing the positions of the grid in the order you visited them.

Example 1:

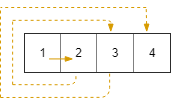
Input: rows = 1, cols = 4, rStart = 0, cStart = 0 Output: [[0,0],[0,1],[0,2],[0,3]]

Example 2:

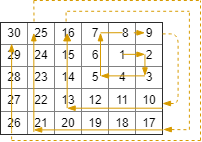
Input: rows = 5, cols = 6, rStart = 1, cStart = 4 Output: [[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]

Constraints:

• 1 <= rows, cols <= 100
• 0 <= rStart < rows
• 0 <= cStart < cols

Code

Brute Force

Time Complexity: $O((\max (M,N){)}^2)$, Space Complexity: $O(N+M)$

use the code from Spiral Matrix && Spiral Matrix II. 直接從起點開始繞行，當 index 在界內才將之 push_back 到 answer vector。

class Solution {
public:
    vector<vector<int>> spiralMatrixIII(int R, int C, int r0, int c0) {
        vector<vector<int>> dir =  {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // east, south, west, north
        vector<vector<int>> res;  
        int len = 0, d = 0; // move <len> steps in the <d> direction
        res.push_back({r0, c0});
        while (res.size() < R * C) {
            if (d == 0 || d == 2) len++; // when move east or west, the length of path need plus 1 
            for (int i = 0; i < len; i++) {
                r0 += dir[d][0];
                c0 += dir[d][1];
                if (r0 >= 0 && r0 < R && c0 >= 0 && c0 < C) // check valid
                    res.push_back({r0, c0});
            }
            d = (d + 1) % 4; // turn to next direction
        }
        return res;
    }
};

Source

• Spiral Matrix III - LeetCode