Find the City With the Smallest Number of Neighbors at a Threshold Distance

Description

There are n cities numbered from 0 to n-1. Given the array edges where edges[i] = [from<sub>i</sub>, to<sub>i</sub>, weight<sub>i</sub>] represents a bidirectional and weighted edge between cities from<sub>i</sub> and to<sub>i</sub>, and given the integer distanceThreshold.

Return the city with the smallest number of cities that are reachable through some path and whose distance is at most distanceThreshold, If there are multiple such cities, return the city with the greatest number.

Notice that the distance of a path connecting cities i and j is equal to the sum of the edges’ weights along that path.

Example 1:

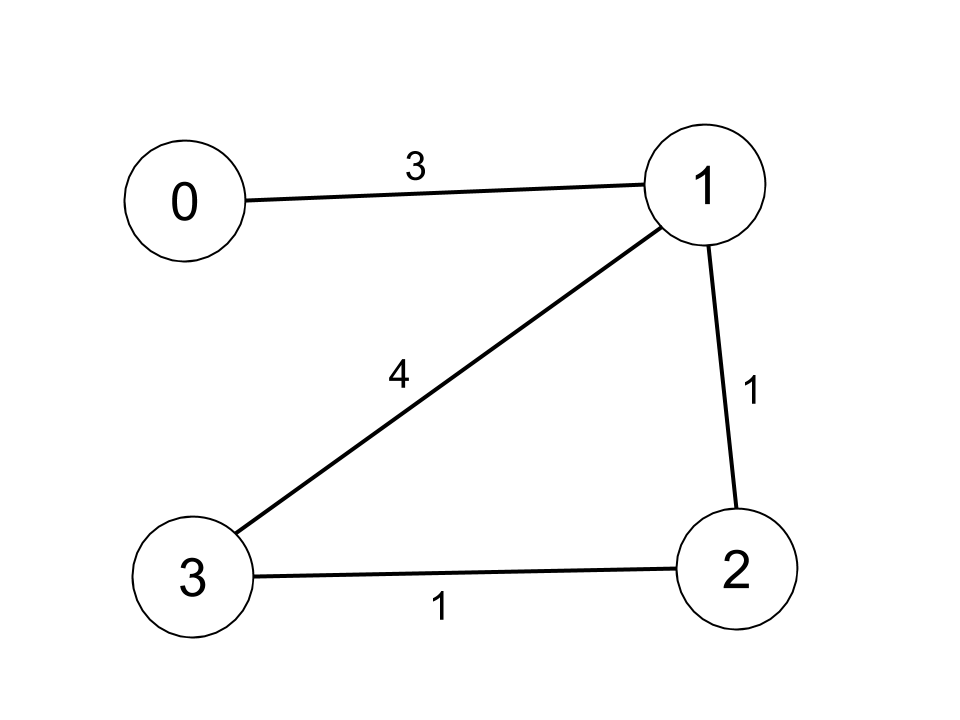
<strong>Input:</strong> n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
<strong>Output:</strong> 3
<strong>Explanation: </strong>The figure above describes the graph.&nbsp;
The neighboring cities at a distanceThreshold = 4 for each city are:
City 0 -&gt; [City 1, City 2]&nbsp;
City 1 -&gt; [City 0, City 2, City 3]&nbsp;
City 2 -&gt; [City 0, City 1, City 3]&nbsp;
City 3 -&gt; [City 1, City 2]&nbsp;
Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.

Example 2:

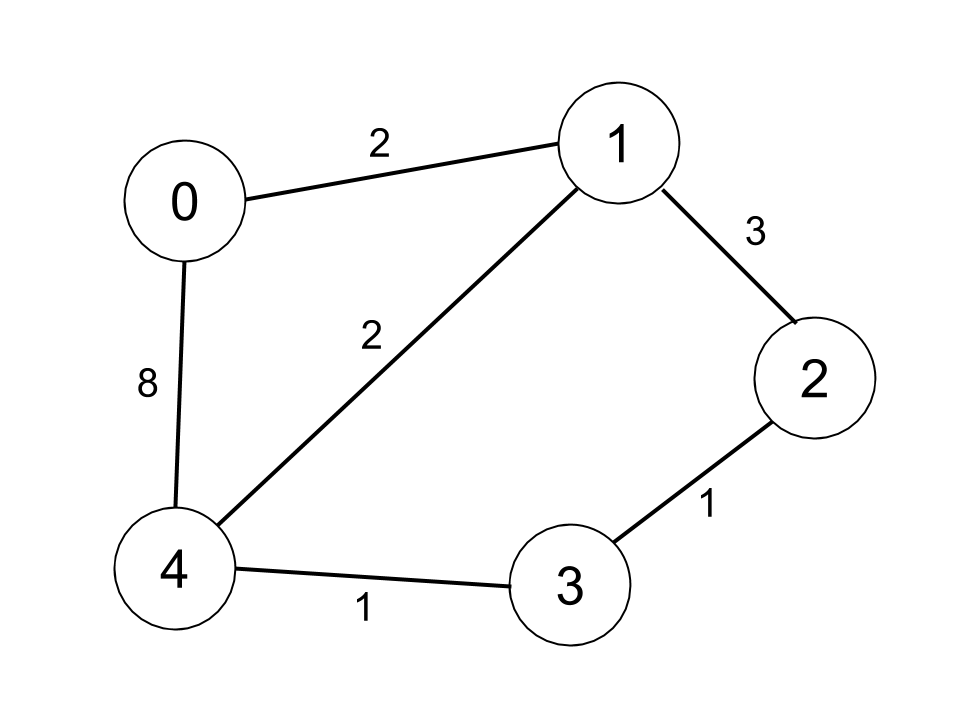
<strong>Input:</strong> n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
<strong>Output:</strong> 0
<strong>Explanation: </strong>The figure above describes the graph.&nbsp;
The neighboring cities at a distanceThreshold = 2 for each city are:
City 0 -&gt; [City 1]&nbsp;
City 1 -&gt; [City 0, City 4]&nbsp;
City 2 -&gt; [City 3, City 4]&nbsp;
City 3 -&gt; [City 2, City 4]
City 4 -&gt; [City 1, City 2, City 3]&nbsp;
The city 0 has 1 neighboring city at a distanceThreshold = 2.

Constraints:

• 2 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= from<sub>i</sub> < to<sub>i</sub> < n
• 1 <= weight<sub>i</sub>, distanceThreshold <= 10^4
• All pairs (from<sub>i</sub>, to<sub>i</sub>) are distinct.

Code

Time Complexity: $O(n^3)$, Space Complexity: $O(n^2)$

see All Pair Shortest Path - Floyd-Warshall。

class Solution {
public:
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        vector<vector<int>> D(n, vector<int>(n, 100000));
        
        for(auto edge: edges) {
            D[edge[0]][edge[1]] = edge[2];
            D[edge[1]][edge[0]] = edge[2];
        }
        
        for(int i = 0; i < n; i++) {
            D[i][i] = 0;
        }
        
        for(int k = 0; k < n; k++) {
            for(int i = 0; i < n; i++) {
                for(int j = 0; j < n ;j++) {
                    if(k == i || k == j) continue;
                    D[i][j] = min(D[i][j], D[i][k] + D[k][j]);
                }
            }
        }
        int answer = INT_MIN;
        int min_neighbors = INT_MAX;
        for(int i = 0; i < n; i++) {
            int neighbors = 0;
            for(int j = 0; j < n; j++) {
                if(D[i][j] <= distanceThreshold) neighbors++;
            } 
            if(neighbors <= min_neighbors) {
                min_neighbors = neighbors;
                answer = i;
            }
        }
        
        return answer;
        
    }
};

DFS(TLE)

Why dfs will TLE?

class Solution {
public:
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        // build adj
        vector<vector<pair<int, int>>> adj(n);
        for(auto edge: edges) {
            int u = edge[0];
            int v = edge[1];
            int w = edge[2];
            adj[u].push_back({v, w});
            adj[v].push_back({u, w});
        }
 
        int res = -1;
        int min_neighbors = n;
        for(int i = 0; i < n; i++) {
            vector<bool> visited(n, false);
            vector<bool> added(n, false);
            int neighbors = travel(i, adj, visited, added, 0, distanceThreshold);
            if(neighbors <= min_neighbors) {
                res = i;
                min_neighbors = neighbors;
            }
        }
        return res;
    }
 
    int travel(int node, vector<vector<pair<int, int>>>& adj, vector<bool>& visited, vector<bool>& added, int curDis, int distanceThreshold) {
        if(visited[node])
            return 0;
 
        visited[node] = true;
        int neighbors = added[node] ? 0 : 1;
        added[node] = true;
        for(auto neighbor_info: adj[node]) {
            int v = neighbor_info.first;
            int w = neighbor_info.second;
            if(curDis + w <= distanceThreshold) {
                int valid = travel(v, adj, visited, added, curDis + w, distanceThreshold);
                neighbors += valid;
                cout << node << " add: " << v << " " << valid << endl;
            }
        }
        visited[node] = false;
        return neighbors;
    }
};

Source

• Find the City With the Smallest Number of Neighbors at a Threshold Distance - LeetCode