Minimum Number of Increments on Subarrays to Form a Target Array

Description

You are given an integer array target. You have an integer array initial of the same size as target with all elements initially zeros.

In one operation you can choose any subarray from initial and increment each value by one.

Return the minimum number of operations to form a target array from initial.

The test cases are generated so that the answer fits in a 32-bit integer.

Example 1:

Input: target = [1,2,3,2,1] Output: 3 Explanation: We need at least 3 operations to form the target array from the initial array. [0,0,0,0,0] increment 1 from index 0 to 4 (inclusive). [1,1,1,1,1] increment 1 from index 1 to 3 (inclusive). [1,2,2,2,1] increment 1 at index 2. [1,2,3,2,1] target array is formed.

Example 2:

Input: target = [3,1,1,2] Output: 4 Explanation: [0,0,0,0] → [1,1,1,1] → [1,1,1,2] → [2,1,1,2] → [3,1,1,2]

Example 3:

Input: target = [3,1,5,4,2] Output: 7 Explanation: [0,0,0,0,0] → [1,1,1,1,1] → [2,1,1,1,1] → [3,1,1,1,1] → [3,1,2,2,2] → [3,1,3,3,2] → [3,1,4,4,2] → [3,1,5,4,2].

Constraints:

• 1 <= target.length <= 105
• 1 <= target[i] <= 105

Code

Brute Force (TLE)

Time Complexity: $O(\max (target))$, Space Complexity: $O(1)$

class Solution {
public:
    int minNumberOperations(vector<int>& target) {
        int res = 0;
        int n = target.size();
        int i;
        while(true) {
            
            int minimum = INT_MAX;
            for(i = 0; i < n; i++) {
                if(target[i] != 0)
                    minimum = min(minimum, target[i]);
            }
            if(minimum == INT_MAX) break;
 
            i = 0;
            while(i < n && target[i] == 0) i++;
            if(i == n) break;
            while(i < n && target[i] > 0) {
                target[i] -= minimum;
                i++;
            }
            
            res += minimum;
        }
        return res;
    }
};

Greedy

Time Complexity: $O(n)$, Space Complexity: $O(1)$

Let us assume that target represents height of columns on a square grid. One operation corresponds to laying out continuous row of bricks. What is the number of these rows? To find this number we count the number of left edges of these rows.

Example: [3,1,5,4,2,3,4,2]. Left edges are marked by red color. Total number of left edges is 3 + 4 + 1 + 1.

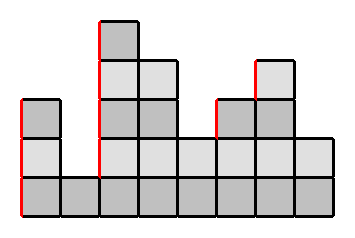
Applying this approach we get

int minNumberOperations(vector<int>& target)
{
    int count = target[0];
    for (int i = 1; i < target.size(); i++)
        count += max(target[i] - target[i - 1], 0);
    return count;
}

Source

• Minimum Number of Increments on Subarrays to Form a Target Array - LeetCode