Spiral Matrix IV

Description

You are given two integers m and n, which represent the dimensions of a matrix.

You are also given the head of a linked list of integers.

Generate an m x n matrix that contains the integers in the linked list presented in spiral order (clockwise), starting from the top-left of the matrix. If there are remaining empty spaces, fill them with -1.

Return the generated matrix.

Example 1:

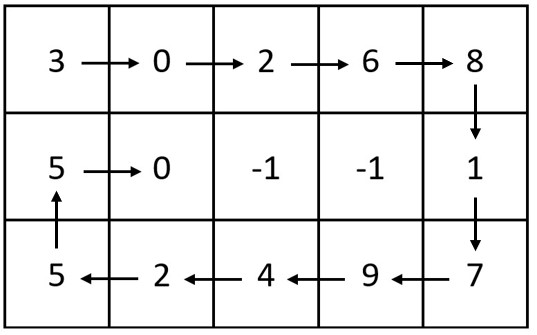
Input: m = 3, n = 5, head = [3,0,2,6,8,1,7,9,4,2,5,5,0] Output: [[3,0,2,6,8],[5,0,-1,-1,1],[5,2,4,9,7]] Explanation: The diagram above shows how the values are printed in the matrix. Note that the remaining spaces in the matrix are filled with -1.

Example 2:

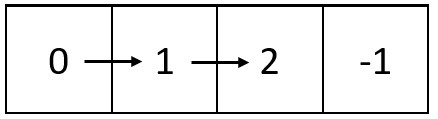
Input: m = 1, n = 4, head = [0,1,2] Output: 0,1,2,-1 Explanation: The diagram above shows how the values are printed from left to right in the matrix. The last space in the matrix is set to -1.

Constraints:

• 1 <= m, n <= 105
• 1 <= m * n <= 105
• The number of nodes in the list is in the range [1, m * n].
• 0 <= Node.val <= 1000

Code

Time Complexity: $O(N+M)$, Space Complexity: $O(N+M)$

Reuse the code from Spiral Matrix II.

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> spiralMatrix(int m, int n, ListNode* head) {
        vector<vector<int>> dir = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        vector<vector<int>> answer(m, vector<int>(n, 0));
 
        vector<int> directionalSteps = {n, m - 1};
        int dir_idx = 0;
        int i = 0, j = -1;
        int count = 1;
        while(directionalSteps[dir_idx % 2]){
 
            for(int k = 0; k < directionalSteps[dir_idx % 2]; k++) {
                i += dir[dir_idx][0];
                j += dir[dir_idx][1];
                if(head) {
                    answer[i][j] = head->val;
                    head = head->next;
                } else {
                    answer[i][j] = -1;
                }
                    
            }
            directionalSteps[dir_idx % 2]--;
            dir_idx = (dir_idx + 1) % 4;
        }
 
        return answer;
    }
};

Source

• Spiral Matrix IV - LeetCode