Description
There are several squares being dropped onto the X-axis of a 2D plane.
You are given a 2D integer array positions where positions[i] = [left<sub>i</sub>, sideLength<sub>i</sub>] represents the i<sup>th</sup> square with a side length of sideLength<sub>i</sub> that is dropped with its left edge aligned with X-coordinate left<sub>i</sub>.
Each square is dropped one at a time from a height above any landed squares. It then falls downward (negative Y direction) until it either lands on the top side of another square or on the X-axis. A square brushing the left/right side of another square does not count as landing on it. Once it lands, it freezes in place and cannot be moved.
After each square is dropped, you must record the height of the current tallest stack of squares.
Return an integer array ans where ans[i] represents the height described above after dropping the i<sup>th</sup> square.
Example 1:
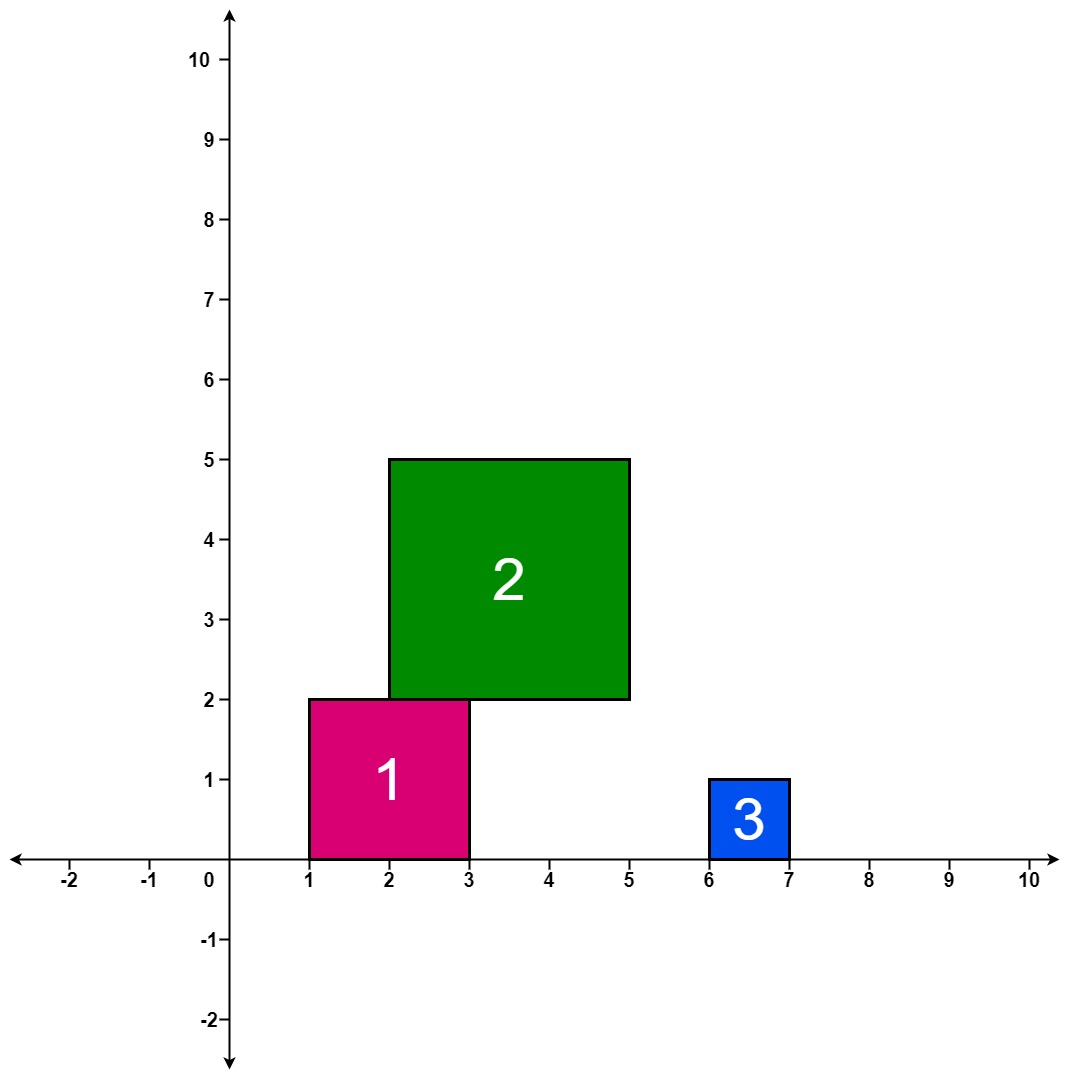
<strong>Input:</strong> positions = [[1,2],[2,3],[6,1]]
<strong>Output:</strong> [2,5,5]
<strong>Explanation:</strong>
After the first drop, the tallest stack is square 1 with a height of 2.
After the second drop, the tallest stack is squares 1 and 2 with a height of 5.
After the third drop, the tallest stack is still squares 1 and 2 with a height of 5.
Thus, we return an answer of [2, 5, 5].
Example 2:
<strong>Input:</strong> positions = [[100,100],[200,100]]
<strong>Output:</strong> [100,100]
<strong>Explanation:</strong>
After the first drop, the tallest stack is square 1 with a height of 100.
After the second drop, the tallest stack is either square 1 or square 2, both with heights of 100.
Thus, we return an answer of [100, 100].
Note that square 2 only brushes the right side of square 1, which does not count as landing on it.
Constraints:
1 <= positions.length <= 10001 <= left<sub>i</sub> <= 10<sup>8</sup>1 <= sideLength<sub>i</sub> <= 10<sup>6</sup>
Code
Time Complexity: , Space Complexity:
類似 The Skyline Problem。可以像 The Skyline Problem 中一樣把融合後的圖畫出來,看看哪些點是我們需要的,會比較好理解。
Map[i] -> k 代表從 index i 開始高度為 j,直到下一個 entry Map[j] -> l ,也就是 index j (j > i) 開始,高度變為 l。
對於一個要落下的 square 來說,使用 lower_bound 來找左右邊界會遇到的(已經落下的 square)。
左邊找到的 square 其左邊界大於等於要落下的 square 的左邊界,如果剛好等於,代表其前一個 square 的右邊界小於要落下的 square 的左邊界,故不影響落下時高度的計算;但若大於,我們就必須檢查其前一個,因為其前一個 square 的右邊界有可能大於在要落下的 square 的左邊界。
右邊找到的 square 其左邊界大於等於要落下的 square 的右邊界,不管剛好相等還是大於,都不會影響要落下 square 的高度計算。
而當一個 square 落下後,右邊界需要檢查:
if(r < r_ptr->first)
mp[r] = tmp;也就是說只有當右邊的 square 的左邊界 index 和落下的 square 的右邊界 index 重合時,我們才不需要 insert 一個 entry,因為右邊的 square 的左邊界已經是一個 entry 了,且根據
Map[i] -> k 代表從 index i 開始高度為 j,直到下一個 entry Map[j] -> l ,也就是 index j (j > i) 開始,高度變為 l。
這個定義,右邊的 square 的左邊界在這個情況下就是我們要的定義,落下的 square 的右邊界無論高低都不是我們要的。
class Solution {
public:
vector<int> fallingSquares(vector<vector<int>>& positions) {
map<int, int> mp;
mp[0] = 0;
mp[INT_MAX] = 0;
vector<int> results;
int cur = 0;
for(auto p: positions) {
auto l = p[0], r = p[0] + p[1], h = p[1];
auto l_ptr = mp.lower_bound(l); // >= l
auto r_ptr = mp.lower_bound(r); // >= r
int tmp = prev(r_ptr)->second;
auto ptr = l_ptr->first == l ? l_ptr : prev(l_ptr);
int maxH = 0;
while(ptr != r_ptr) {
maxH = max(maxH, ptr->second);
ptr = next(ptr);
}
if(l_ptr != r_ptr)
mp.erase(l_ptr, r_ptr);
mp[l] = maxH + h;
if(r < r_ptr->first)
mp[r] = tmp;
cur = max(cur, maxH + h);
results.push_back(cur);
}
return results;
}
};