Stone Game IV

Description

Alice and Bob take turns playing a game, with Alice starting first.

Initially, there are n stones in a pile. On each player’s turn, that player makes a move consisting of removing any non-zero square number of stones in the pile.

Also, if a player cannot make a move, he/she loses the game.

Given a positive integer n, return true if and only if Alice wins the game otherwise return false, assuming both players play optimally.

Example 1:

Input: n = 1 Output: true Explanation: Alice can remove 1 stone winning the game because Bob doesn’t have any moves.

Example 2:

Input: n = 2 Output: false Explanation: Alice can only remove 1 stone, after that Bob removes the last one winning the game (2 → 1 → 0).

Example 3:

Input: n = 4 Output: true Explanation: n is already a perfect square, Alice can win with one move, removing 4 stones (4 → 0).

Constraints:

• 1 <= n <= 105

Code

DP - recursion with memoization

First understand this problem with an example. Take n = 7 where n denotes no. of stone

As, Alice always start game first to remove stone. So, how many choices can he make to remove 7 stones is:

1 ^ 1 = 1
2 ^ 2 = 4

So, he can only make 2 choices

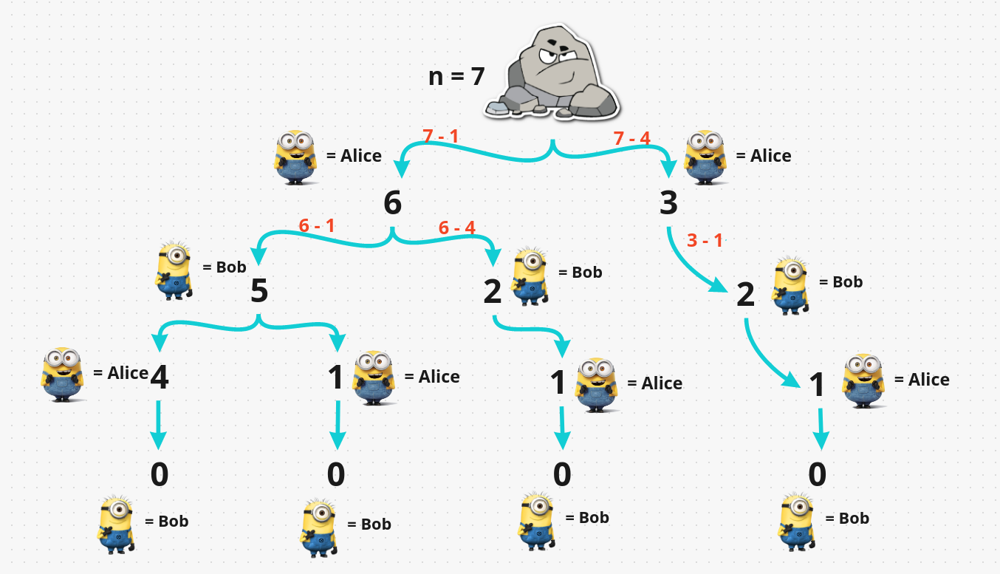
• So, from 7 stones Alice 1st remove 1 stone & then Alice remove 4 stones
• • When Alice remove 1 stone the remaining stone left is 6.
• • But If Alice remove 4 stones then remaining stones left are 3.
• Now it's Bob turn. Bob as well can make only 2 moves i.e. 1 OR 4 which is less than 6
• • When Bob remove 1 stone from branch 6 the remaining stone left is 5. But If Bob remove 4 stones from branch 6 then remaining stones left are 2.
• • But in Branch 3 Bob can only remove 1 stone, so remaining left is 2.
• Now it's Alice turn.
• • From branch 5 if Alice decide to remove 1 stone remaining stone left is 4. But, if alice decide to remove 4 stone remaining stone left is 1.
• • From branch 2 if Alice decide to remove 1 stone remaining stone left is 1.
• • From another branch 2 if Alice decide to remove 1 stone remaining stone left is 1
• Now the Bob turn and every branch is ending with perfect square. So, Bob can remove from any branch because there is no branch from Alice can win.

So, as you see there are no. of repeated sub problems, like 2, 4 so we will use the Dynamic Programming to solve this problem.

Time Complexity: $O(n)$, Space Complexity: $O(n)$

class Solution {
    int memo[100001] = {};
public:
    bool winnerSquareGame(int n) {
        if(n == 0) return false;
        if(n == 1) return true;
        if(memo[n] != 0) return memo[n];
        int x = sqrt(n);
        if(x * x == n) return true;
 
        bool win = false;
        for(int i = 1; i * i <= n; i++) {
            if(!winnerSquareGame(n - i * i)) {
                win = true;
                break;
            }
        }
        return memo[n] = win;
    }
 
};

Source

• Stone Game IV - LeetCode