Description
Given the root of a binary tree, return the maximum width of the given tree.
The maximum width of a tree is the maximum width among all levels.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is guaranteed that the answer will in the range of a 32-bit signed integer.
Example 1:
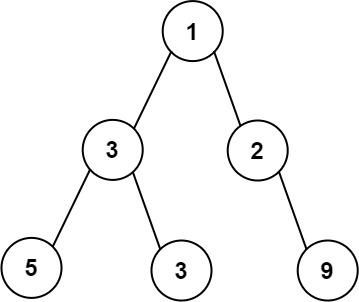
Input: root = [1,3,2,5,3,null,9] Output: 4 Explanation: The maximum width exists in the third level with length 4 (5,3,null,9).
Example 2:
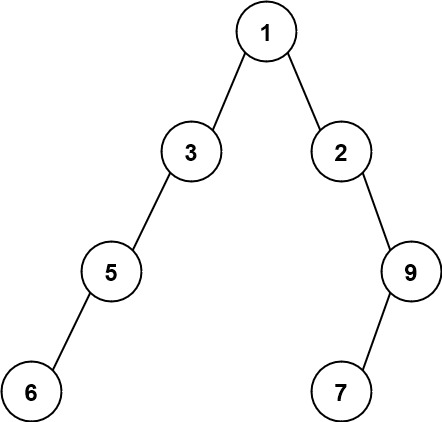
Input: root = [1,3,2,5,null,null,9,6,null,7] Output: 7 Explanation: The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
Example 3:
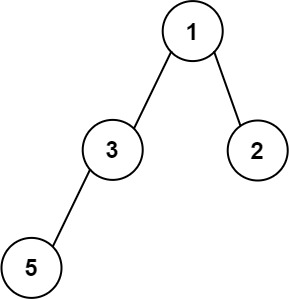
Input: root = [1,3,2,5] Output: 2 Explanation: The maximum width exists in the second level with length 2 (3,2).
Constraints:
- The number of nodes in the tree is in the range
[1, 3000]. -100 <= Node.val <= 100
Code
Level Order Traversal
比較每一層的 index 的最大和最小,因為 index 每隔一層就會是兩倍(2i + 1, 2i + 2)因此做法需要用到 unsigned long long,較難 handle 很深的 test case。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
queue<pair<TreeNode*, unsigned long long>> q;
q.push({root, 0});
int maxWidth = 0;
while(!q.empty()) {
int levelSize = q.size();
unsigned long long levelMinIndex = ULLONG_MAX;
unsigned long long levelMaxIndex = 0;
for(int i = 0; i < levelSize; i++) {
auto node = q.front().first;
auto index = q.front().second;
levelMinIndex = min(levelMinIndex, index);
levelMaxIndex = max(levelMaxIndex, index);
q.pop();
if(node->left) q.push({node->left, 2*index + 1});
if(node->right) q.push({node->right, 2*index + 2});
}
maxWidth = max(maxWidth, (int)(levelMaxIndex - levelMinIndex + 1));
}
return maxWidth;
}
};因此我們需要想辦法避免 interger overflow 這件事情。
關鍵在於將每一層的開頭的 node 的 index 都設為 0:int index = q.front().second - start;
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
queue<pair<TreeNode*, int>> q;
q.push({root, 0});
int maxWidth = 0;
while(!q.empty()) {
int levelSize = q.size();
int start = q.front().second;
int end = q.back().second;
maxWidth = max(maxWidth, end - start + 1);
for(int i = 0; i < levelSize; i++) {
auto node = q.front().first;
int index = q.front().second - start;
q.pop();
if(node->left) q.push({node->left, (long long) 2*index + 1});
if(node->right) q.push({node->right, (long long) 2*index + 2});
}
}
return maxWidth;
}
};