Critical Connections in a Network

Description

There are n servers numbered from 0 to n - 1 connected by undirected server-to-server connections forming a network where connections[i] = [ai, bi] represents a connection between servers ai and bi. Any server can reach other servers directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some servers unable to reach some other server.

Return all critical connections in the network in any order.

Example 1:

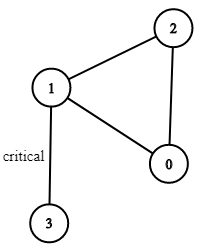
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]] Output: 1,3 Explanation: 3,1 is also accepted.

Example 2:

Input: n = 2, connections = 0,1 Output: 0,1

Constraints:

• 2 <= n <= 105
• n - 1 <= connections.length <= 105
• 0 <= ai, bi <= n - 1
• ai != bi
• There are no repeated connections.

Code

Tarjan’s Algorithm

Time Complexity: $O(n+m)$, Space Complexity: $O(n+m)$

• Finding bridges in a graph in O(N+M)
• Tarjan’s Algorithm

class Solution {
    vector<vector<int>> adj;
    vector<vector<int>> res;
    int time = 0;
public:
    vector<vector<int>> criticalConnections(int n, vector<vector<int>>& connections) {
        adj.resize(n);
        for(auto conn: connections) {
            adj[conn[0]].emplace_back(conn[1]);
            adj[conn[1]].emplace_back(conn[0]);
        }
 
        vector<int> visited(n, 0);
        vector<int> parent(n, -1);
        vector<int> dfn(n, 0);
        vector<int> low(n, 0);
        for(int i = 0; i < n; i++) {
            if(!visited[i]) dfs(i, visited, dfn, low, parent);
        }
 
        return res;
    }
 
    void dfs(int u, vector<int>& visited, vector<int>& dfn, vector<int>& low, vector<int>& parent) {
        visited[u] = 1;
        dfn[u] = low[u] = time++;
 
        for(int v: adj[u]) {
            if(v == parent[u]) continue;
            if(!visited[v]) {
                parent[v] = u;
                dfs(v, visited, dfn, low, parent);
 
                if(low[v] > dfn[u]) res.push_back({u, v});
                
                low[u] = min(low[u], low[v]);
            } else {
                low[u] = min(low[u], dfn[v]);
            }
        }
    }
};

Source

• Critical Connections in a Network - LeetCode