Recover Binary Search Tree

Description

Topics

Companies

You are given the root of a binary search tree (BST), where the values of exactly two nodes of the tree were swapped by mistake. Recover the tree without changing its structure.

Example 1:

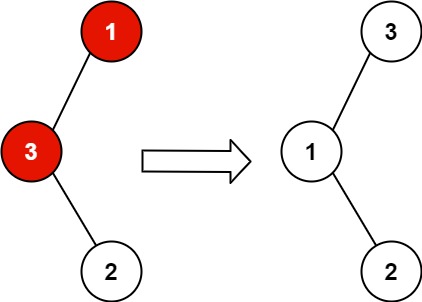
Input: root = [1,3,null,null,2] Output: [3,1,null,null,2] Explanation: 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.

Example 2:

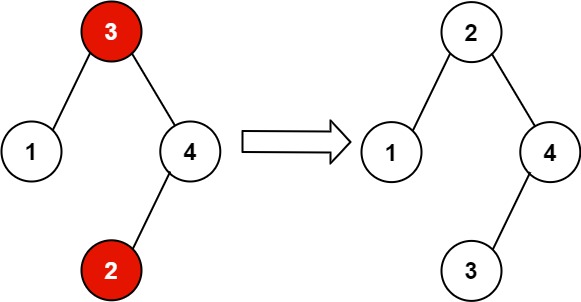
Input: root = [3,1,4,null,null,2] Output: [2,1,4,null,null,3] Explanation: 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.

Constraints:

• The number of nodes in the tree is in the range [2, 1000].
• -231 <= Node.val <= 231 - 1

Follow up: A solution using O(n) space is pretty straight-forward. Could you devise a constant O(1) space solution?

Code

KEY: 正確的 Binary Search Tree 的 inorder traversal 會是 sorted 。

要注意 The first element is always larger than its next one while the second element is always smaller than its previous one.

Time Complexity: $O(n)$, Space Complexity: $O(1)$

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* firstError = nullptr;
    TreeNode* secondError = nullptr;
    TreeNode* prev = new TreeNode(INT_MIN);
    void recoverTree(TreeNode* root) {
        inorder_traversal(root);
        swap(firstError->val, secondError->val);
    }
 
    void inorder_traversal(TreeNode* node) {
        if(!node)
            return;
        
        inorder_traversal(node->left);
 
        if(firstError == nullptr && prev->val >= node->val)
            firstError = prev;
        if(firstError != nullptr && prev->val >= node->val)
            secondError = node;
 
        prev = node;
        inorder_traversal(node->right);
    }
};

Source

• Recover Binary Search Tree - LeetCode