Number of Islands

Description

You are given an m x n binary matrix grid. An island is a group of 1’s (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

The area of an island is the number of cells with a value 1 in the island.

Return the maximum area of an island in grid. If there is no island, return 0.

Example 1:

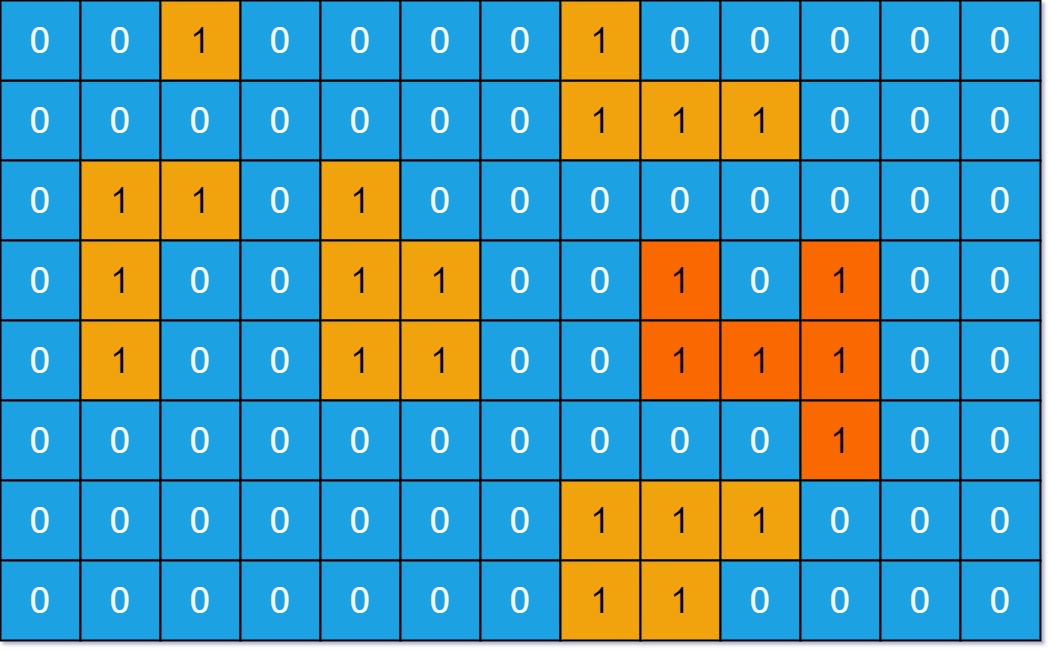
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] Output: 6 Explanation: The answer is not 11, because the island must be connected 4-directionally.

Example 2:

Input: grid = 0,0,0,0,0,0,0,0 Output: 0

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• grid[i][j] is either 0 or 1.

Code

code 的邏輯和 Flood Fill 大同小異。 Time Complexity: $O(n+m)$, Space Complexity: $O(n+m)$

BFS

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int island = 0;
        vector<int> dir = {0, 1, 0, -1, 0};
        int n = grid.size(), m = grid[0].size();
       for(int i = 0; i < grid.size(); i++) {
           for(int j = 0; j < grid[i].size(); j++) {
               if(grid[i][j] == '1') {
                   grid[i][j] = '0';
                   island++;
                   queue<pair<int, int>> q;
                   q.push({i, j});
                   while(!q.empty()) {
                       auto p = q.front();
                       q.pop();
                       for(int k = 0; k < 4; k++) {
                           int x = p.first + dir[k], y = p.second + dir[k + 1];
                           if(x >= 0 && x < n && y >= 0 && y < m && grid[x][y] == '1') {
                               grid[x][y] = '0';
                               q.push({x, y});
                           }
                       }
                   }
               }
           }
       } 
       return island;
    }
};

DFS

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int n = grid.size();
        int m = grid[0].size();
        vector<vector<int>> visited(n, vector<int>(m, 0));
        int count = 0;
        for(int i = 0; i < n; i++) {
            for(int j = 0; j < m; j++) {
                if(!visited[i][j] && grid[i][j] == '1') {
                    count++;
                    dfs(i, j, visited, grid);
                }
            }
        }
        return count;
    }
 
    void dfs(int x, int y, vector<vector<int>>& visited, vector<vector<char>>& grid) {
        visited[x][y] = 1;
        int n = grid.size();
        int m = grid[0].size();
        if(x + 1 < n && !visited[x+1][y] && grid[x+1][y] == '1') dfs(x+1, y, visited, grid);
        if(x - 1 >= 0 && !visited[x-1][y] && grid[x-1][y] == '1') dfs(x-1, y, visited, grid);
        if(y + 1 < m && !visited[x][y + 1] && grid[x][y + 1] == '1') dfs(x, y+1, visited, grid);
        if(y - 1 >= 0 && !visited[x][y - 1] && grid[x][y - 1] == '1') dfs(x, y-1, visited, grid);
        return;
    }
};

• Number of Islands - LeetCode