Minimum Height Trees

Description

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h))  are called minimum height trees (MHTs).

Return a list of all MHTs’ root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

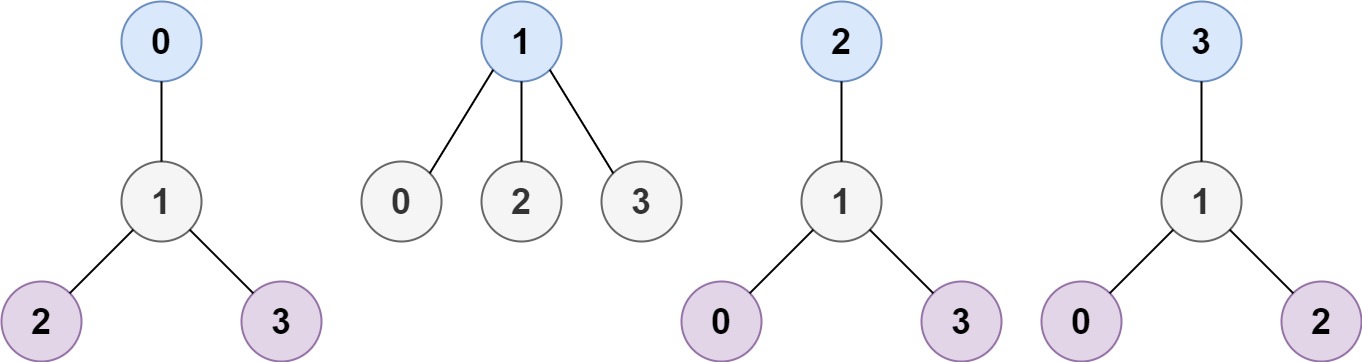
Input: n = 4, edges = [[1,0],[1,2],[1,3]] Output: [1] Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

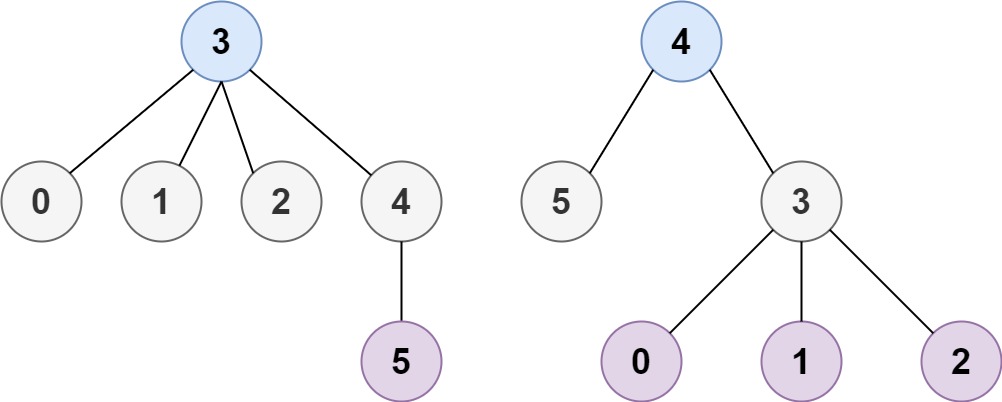
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]] Output: [3,4]

Constraints:

• 1 <= n <= 2 * 104
• edges.length == n - 1
• 0 <= ai, bi < n
• ai != bi
• All the pairs (ai, bi) are distinct.
• The given input is guaranteed to be a tree and there will be no repeated edges.

Code

1. There are at most 2 (node as root) MHT, if there are 3, then the middle one will be the only one that forms MHT.
2. The further a node is from a leaf, the better.

總和上述兩點觀察，我們使用 topological sort 的概念依照 indegree 大小由 leaf node 開始往內走，紀錄每一層所遇到的 nodes，回傳最後一層的 nodes，即是所求。

Topological Sort

class Solution {
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        
        if(n == 0)
            return {};
        if(n == 1)
            return {0};
        
        vector<vector<int>> adj(n);
        vector<int> inDegree(n, 0);
        for(auto edge: edges) {
            adj[edge[0]].push_back(edge[1]);
            adj[edge[1]].push_back(edge[0]);
            inDegree[edge[0]]++;
            inDegree[edge[1]]++;
        }   
 
        queue<int> q;
        for(int i = 0; i < n; i++) {
            // leaf node
            if(inDegree[i] == 1) {
                q.push(i);
            }
        }
 
        vector<int> res;
        while(!q.empty()) {
            res.clear();
            int levelSize = q.size();
            for(int i = 0; i < levelSize; i++) {
                auto node = q.front(); q.pop();
                res.push_back(node);
                for(auto neighbor: adj[node]) {
                    inDegree[neighbor]--;
                    if(inDegree[neighbor] == 1) {
                        q.push(neighbor);
                    }
                }
            }
        }
        
        return res;
 
    }
 
};

Source

• Minimum Height Trees - LeetCode