Search a 2D Matrix

Description

You are given an m x n integer matrix matrix with the following two properties:

• Each row is sorted in non-decreasing order.
• The first integer of each row is greater than the last integer of the previous row.

Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity.

Example 1:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 Output: true

Example 2:

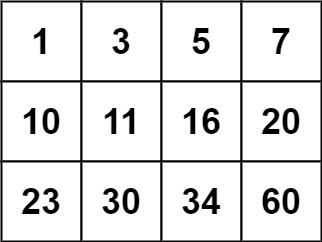
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 Output: false

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

Code

Time Complexity: $O(\log mn)$, Space Complexity: $O(1)$

基本概念：Binary Search 101

這題就是 Classic Binary Search 的 2D 版本而已。

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int l = 0, r = m * n - 1;
        while(l < r) {
            int mid = l + (r - l) / 2;
            int i = mid / n;
            int j = mid % n;
            if(matrix[i][j] >= target) r = mid;
            else l = mid + 1;
        }
        return matrix[l / n][l % n] == target;
    }
};

Link

• Search a 2D Matrix