Check if a Parentheses String Can Be Valid

Description

A parentheses string is a non-empty string consisting only of '(' and ')'. It is valid if any of the following conditions is true:

• It is ().
• It can be written as AB (A concatenated with B), where A and B are valid parentheses strings.
• It can be written as (A), where A is a valid parentheses string.

You are given a parentheses string s and a string locked, both of length n. locked is a binary string consisting only of '0's and '1's. For each index i of locked,

• If locked[i] is '1', you cannot change s[i].
• But if locked[i] is '0', you can change s[i] to either '(' or ')'.

Return true if you can make s a valid parentheses string. Otherwise, return false.

Example 1:

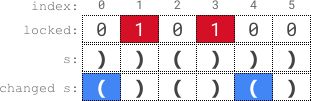
Input: s = ”))()))”, locked = “010100” Output: true Explanation: locked[1] '1' and locked[3] ‘1’, so we cannot change s[1] or s[3]. We change s[0] and s[4] to ’(’ while leaving s[2] and s[5] unchanged to make s valid.

Example 2:

Input: s = ”()()”, locked = “0000” Output: true Explanation: We do not need to make any changes because s is already valid.

Example 3:

Input: s = ”)”, locked = “0” Output: false Explanation: locked permits us to change s[0]. Changing s[0] to either ’(’ or ’)’ will not make s valid.

Constraints:

• n == s.length == locked.length
• 1 <= n <= 105
• s[i] is either '(' or ')'.
• locked[i] is either '0' or '1'.

Code

為什麼要做兩遍？

• Left-to-right check ensures that we do not have orphan ’)’ parentheses.
• Right-to-left checks for orphan ’(’ parentheses.

要注意由左到右以及由右到左時的 close & open 分別對應不同開口方向。

要注意結構是 if, else if, else if，若一個 index 是 unlocked 就不計入 open or close，因為我們可以將自由的格子任意改成 open or close（看情況），所以判斷 unlock 的 case 要寫在最上面！

class Solution {
public:
    bool canBeValid(string s, string locked) {
	    // edge case, e.g. s = '('
        if (s.length() % 2 == 1) 
            return false;
 
        int open = 0, close = 0, unlock = 0, unpaired = 0;
        for(int i = 0; i < s.length(); i++) {
            if(locked[i] == '0') {
                unlock++;
            } else if (s[i] == '(') {
                open++;
            } else if (s[i] == ')') {
                close++;
            }
            // check step by step
            unpaired = close - open;
            if(unpaired > unlock) return false;
        }
 
        // counter example for not checking from right to left
        // "())(()(()(())()())(())((())(()())((())))))(((((((())(()))))("
        // "100011110110011011010111100111011101111110000101001101001111"
 
        open = 0, close = 0, unlock = 0, unpaired = 0;
        for(int i = s.length() - 1; i >= 0; i--) {
            if(locked[i] == '0') {
                unlock++;
            } else if (s[i] == ')') {
                open++;
            } else if (s[i] == '(') {
                close++;
            }
            // check step by step
            unpaired = close - open;
            if(unpaired > unlock) return false;
        }
 
 
        return true;
        
    }
};
 
 

Source

• Check if a Parentheses String Can Be Valid - LeetCode