Description

An attendance record for a student can be represented as a string where each character signifies whether the student was absent, late, or present on that day. The record only contains the following three characters:

'A': Absent.
'L': Late.
'P': Present.

Any student is eligible for an attendance award if they meet both of the following criteria:

The student was absent ('A') for strictly fewer than 2 days total.
The student was never late ('L') for 3 or more consecutive days.

Given an integer n, return the number of possible attendance records of length n that make a student eligible for an attendance award. The answer may be very large, so return it modulo 109 + 7.

Example 1:

Input: n = 2 Output: 8 Explanation: There are 8 records with length 2 that are eligible for an award: “PP”, “AP”, “PA”, “LP”, “PL”, “AL”, “LA”, “LL” Only “AA” is not eligible because there are 2 absences (there need to be fewer than 2).

Example 2:

Input: n = 1 Output: 3

Example 3:

Input: n = 10101 Output: 183236316

Constraints:

1 <= n <= 105

Code

Top Down DP with Memoization

Time Complexity: $O (n)$ , Space Complexity: $O (n)$

class Solution {
    long mod = 1e9 + 7;
public:
    int checkRecord(int n) {
        vector<vector<vector<int>>> memo(n, vector<vector<int>>(2, vector<int>(3, 0)));
        return dfs(0, 0, 0, n, memo);
    }
 
    int dfs(int i, int A, int L, int n, vector<vector<vector<int>>>& memo) {
        if(i == n) return 1;
        if(memo[i][A][L] != 0) return memo[i][A][L];
        long res = dfs(i + 1, A,  0, n, memo); // P
        if(A == 0) res += dfs(i + 1, A + 1, 0, n, memo); // A
        if(L < 2) res += dfs(i + 1, A, L + 1, n, memo); // L
 
        return memo[i][A][L] = (int)(res % mod);
    } 
};

Finite State O(log n)

It’s helpful to think of the set of rewardable records as a regular language, and a particular student’s attendence record as belonging to a state in a finite state machine:

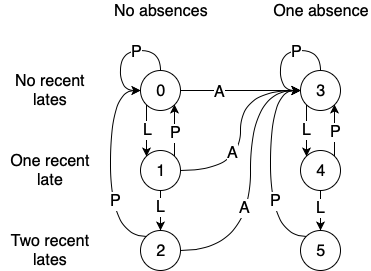
(For example, if you were late today, but not yesterday, and you’ve had no absences so far, then you’re in state 1. If you are late tomorrow, you move to state 2.)

This makes it fairly easy to calculate the number of length-n rewardable records, we can recursively compute the number of length-n records for each of these six states:

Base case: The length-zero record, '', belongs to state 0.
Recursive case: If we add another day to the record length, each state becomes the sum of all the states with an arrow pointing into it.

Expressed algebraically:

We represent the counts for the six states as a vector. For the base-case (n = 0), this is v₀ = [1 0 0 0 0 0]^T.
We represent the finite-state-machine transitions as a matrix, A, where the value of A_ij is the number of arrows from state j to state i:

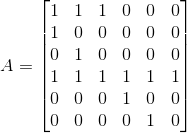
The final counts are v_n = Aⁿ v₀.
We return the sum of the entries of v_n.

We can compute Aⁿ in O(log n) time, as per problem #50:

Compute (A¹, A², A⁴, A⁸, …) by repeatedly replacing A with A².
Then Aⁿ is the product of all the A^{2^i} for which the i‘th bit of the little-endian binary representation of n is 1.

Implementation

For convenience, I’ll be using the numpy library.

import numpy as np

We represent the state counts as a vector:

initial_counts = np.array(
    [1, 0, 0, 0, 0, 0], 
    dtype=np.int64
)

And the finite state machine as an adjacency matrix (the number at (i, j) being the number of arrows from state j to state i):

adjacency_matrix = np.array([
    [1, 1, 1, 0, 0, 0],
    [1, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0],
    [1, 1, 1, 1, 1, 1],
    [0, 0, 0, 1, 0, 0],
    [0, 0, 0, 0, 1, 0],
], dtype=np.int64)

We now just left-multiply initial_counts by adjacency_matrix n times — equivalent to left-multiplying initial_counts by power(adjacency_matrix, n) (the symbol @ is the NumPy operator for matrix multiplication):

final_counts = power(adjacency_matrix, n) @ initial_counts

And finally, return the sum of the counts, modulo 10**9 + 7:

MODULUS = 10**9 + 7
return sum(final_counts) % MODULUS

It’s in the implementation of the power function that we can take the algorithm from O(n) to O(log n). The simple way to take the power of a matrix would be to start with an identity matrix, then multiply it by the matrix n times (taking the remainder mod MODULUS each time to avoid overflow):

def power(A, exp):
    B = np.identity(len(A), dtype=np.int64)
for _ in range(exp):
    B = B @ A
B %= MODULUS
    return B

Instead, we separate the exponent into a sum of powers of 2 (its binary representation), then multiply in A raised to those powers of 2.

def power(A, exp):
    B = np.identity(len(A), dtype=np.int64)
    for bit in reversed(bin(exp)[2:]):
        if bit == '1':
            B = B @ A
            B %= MODULUS
        A = A @ A
        A %= MODULUS
    return B

Putting it all together:

import numpy as np
 
class Solution:
    
    def checkRecord(self, n: int) -> int:
        MODULUS = 10**9 + 7
 
        initial_counts = np.array(
            [1, 0, 0, 0, 0, 0], 
            dtype=np.int64
        )
 
        adjacency_matrix = np.array([
            [1, 1, 1, 0, 0, 0],
            [1, 0, 0, 0, 0, 0],
            [0, 1, 0, 0, 0, 0],
            [1, 1, 1, 1, 1, 1],
            [0, 0, 0, 1, 0, 0],
            [0, 0, 0, 0, 1, 0],
        ], dtype=np.int64)
 
        def power(A, exp):
            B = np.identity(len(A), dtype=np.int64)
            for bit in reversed(bin(exp)[2:]):
                if bit == '1':
                    B = B @ A
                    B %= MODULUS
                A = A @ A
                A %= MODULUS
            return B
 
        final_counts = power(adjacency_matrix, n) @ initial_counts
 
        return sum(final_counts) % MODULUS

Jimmy Lin's Blog

Explorer

Student Attendance Record II

Description

Code

Top Down DP with Memoization

Finite State O(log n)

Implementation

Source

Graph View

Table of Contents

Backlinks